если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
доказательство:
пусть прямые а и b параллельны и пересечены секущей cd. доказать, что накрест лежащие углы 1 и 2 равны.
предположим, что углы 1 и 2 не равны. тогда от луча cd отложим ∠еcd=∠2 так, чтобы ∠еcd и ∠2 были накрест лежащими углами при пересечении прямых се и b секущей cd.
по построению эти накрест лежащие углы равны, а поэтому прямая cd параллельна прямой b. получили, что через точку с проходят две прямые (а и cе) параллельные прямой b. а это противоречит аксиоме параллельности прямых. следовательно, предположение неверно и угол ∠1=∠2. что и требовалось доказать.
пример.
прямая ав параллельна прямой cd, аd - биссектриса угла bac, а ∠adc=50 градусов. чему равна градусная мера ∠cad?
так как прямые ав и cd параллельны и ad - секущая при этих параллельных прямых, то накрест лежащие углы adc и bad равны. значит, ∠bad=50 градусов.
так как ad - биссектриса ∠bac, то ∠cad=∠bad. следовательно, градусная мера ∠cad=50 градусов.
пример.
прямые ав и cd параллельны. отрезок ав=сd. доказать, что прямая ас параллельна прямой bd.
рассмотрим треугольник abd и треугольник acd.
ав=cd по условию , ad - общая. а углы bad и adc равны как накрест лежащие углы при параллельных прямых ав и cd и секущей аd. следовательно, треугольники abd и acd равны по первому признаку равенства треугольников. а значит, у них соответственные стороны и углы равны.
то есть ∠cad=∠bda. а эти углы являются накрест лежащими при прямых ac и bd и секущей ad. это означает, что прямые ac и bd параллельны. что и требовалось доказать.
пример.
на рисунке ∠cbd=∠adb. доказать, что ∠вса=∠cad.
углы cbd и adb - накрест лежащие углы при прямых ad и bc и секущей bd. а так как эти углы равны, то прямые ad и bc параллельны.
∠вса и ∠cad являются накрест лежащими при параллельных прямых ad и bc и секущей ас, а следовательно, они равны. что и требовалось доказать.
отметим, что если доказана какая-либо теорема, то это не означает, что обратная ей теорема верна.
например, если углы вертикальные, то они равны. а вот если углы равны, то это ещё не означает, что они вертикальные.
1)если две параллельные прямые пересечены секущей, накрест лежащие углы равны.2)если две параллельные прямые пересечены секущей, то соответственные углы равны.3)если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.4)если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.S = √3 ед².
Объяснение:
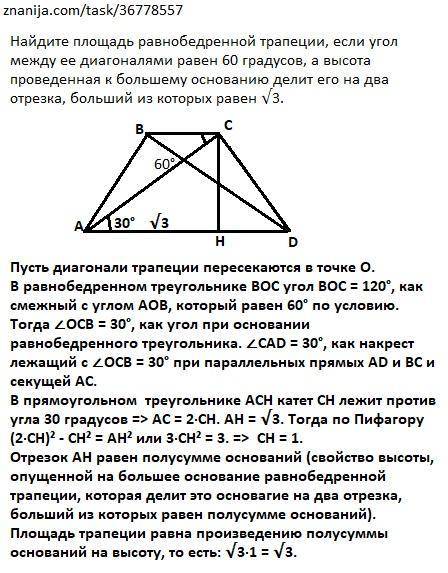
Пусть диагонали трапеции пересекаются в точке О.
В равнобедренном треугольнике ВОС угол ВОС = 120°, как смежный с углом АОВ, который равен 60° по условию. Тогда ∠ОСВ = 30°, как угол при основании равнобедренного треугольника. ∠CAD = 30°, как накрест лежащий с ∠ОСВ = 30° при параллельных прямых AD и ВС и секущей АС.
В прямоугольном треугольнике АСН катет СН лежит против угла 30 градусов => АС = 2·СН. АН = √3. Тогда по Пифагору
(2·СН)² - СН² = АН² или 3·СН² = 3. => СН = 1 ед.
Отрезок АН равен полусумме оснований (свойство высоты, опущенной на большее основание равнобедренной трапеции, которая делит это основание на два отрезка, больший из которых равен полусумме оснований). Итак, полусумма оснований равна √3 (дано). Тогда площадь трапеции равна произведению полусуммы оснований на высоту, то есть: √3·1 = √3 ед².
Тогда периметр может быть
(1+24)×2=50 см
(2+24)×2=52 см
(3+8)×2=22 см
(4+6)×2=20 см