Объяснение:
1. Сумма длин двух любых сторон треугольника всегда должна превышать длину третьей стороны. Пусть первая сторона=х, тогда вторая = х+5.
(х+5)-х<12<(х+5)+х
х+5-х<12<х+5+х
5<12<2х+5
2х+5>12
2х>12-5
2х>7
х>3,5
Следовательно, первая сторона не может быть меньше 3,5см, а вторая сторона не может быть меньше 3,5 + 5 = 8,5см.
2. У равнобедренного треугольника углы при основании равны. Пусть угол А = х, тогда и угол С = х.
х+х+46°=180°
2х=180°-46°
2х=134°
х=134°:2
х=67°.
Угол А= угол С = 67°
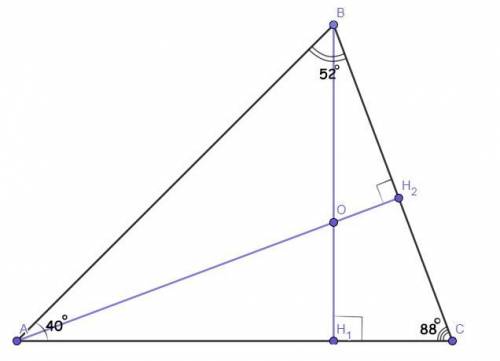
Два угла треугольника равны 40° и 52°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов.
- - -
Дано :ΔАВС.
∠А = 40°.
∠В = 52°.
ВН₁ и АН₂ - высоты.
Точка О - ортоцентр (точка пересечения высот).
Найти :∠АОВ = ? (или ∠Н₁ОН₂, не важно, так как они равны как вертикальные).
Решение :Немного о расположении ортоцентра О :
Для начала найдём ∠С.
По теореме о сумме углов треугольника -
∠А + ∠В + ∠С = 180°
∠С = 180° - ∠А - ∠В
∠С = 180° - 40° - 52°
∠С = 88°.
Так как все углы ΔАВС - острые, то ортоцентр О лежит внутри ΔАВС.
- - -
Рассмотрим ΔСВН₁ - прямоугольный (так как ∠ВН₁С = 90° по определению высоты треугольника).
Сумма острых углов прямоугольного треугольника равна 90°.Тогда -
∠Н₁СВ + ∠Н₁ВС = 90°
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - 88°
∠Н₁ВС = 2°.
Теперь рассмотрим ΔОВН₂ - прямоугольный (так как ∠ОН₂В = 90°).
По выше сказанному -
∠ВОН₂ + ∠ОВН₂ = 90°
∠ВОН₂ = 90° - ∠ОВН₂
∠ВОН₂ = 90° - 2°
∠ВОН₂ = 88°.
- - -
∠ВОН₂ и ∠АОВ - смежные.
Сумма смежных углов равна 180°.Следовательно -
∠ВОН₂ + ∠АОВ = 180°
∠АОВ = 180° - ∠ВОН₂
∠АОВ = 180° - 88°
∠АОВ = 92°.
ответ :92°.
Пусть биссектриса угла CDA пересекает AB в точке M.
Тогда AM/BM = 9/7;
BM = AB*7/(9 + 7) = 7/2; AM = 9/2;
Если провести MN II BC, точка N - на CD, то CN/DN = BM/AM = 7/9; и
DN = 90/16; CN = 70/16;
Так как углы NMD и NDM оба равны углу MDA, треугольник NMD равнобедренный, и DN = MN = 90/16;
Дальше можно опять делать по разному, но суть одна. Например, так.
Пусть CE II AB; точка E - на AD; и СЕ пересекает MN в точке K;
тогда KN = MN - BC = 42/16; и DE/KN = DC/CN;
DE = (42/16)*(16/7) = 6;
Вот тут надо остановиться. Решение конкретной этой задачи уже на ладони :) Треугольник CED имеет стороны DE = 6; CE = 8; CD = 10; это египетский треугольник, то есть CE перпендикулярно AD;
Ясно, что площадь трапеции (в данном случае - прямоугольной трапеции) равна 3*8 + 6*8/2 = 48; (или если охота - основания 3 и 6+3 = 9, высота 8, площадь (3 + 9)*8/2 = 48)
Теперь вопрос - а что делать, если бы сложилось не так хорошо, и трапеция не оказалась бы прямоугольной?
Основания её все равно нашлись - все четыре. Если достроить трапецию до треугольника, продлив боковые стороны, то не сложно найти и все стороны этого треугольника, а также площадь подобного ему треугольника, с основанием BC. Площадь трапеции равна разности их площадей, которые находятся по формуле Герона (достаточно искать площадь одного - треугольники подобны, и коэффициент подобия их равен отношению оснований).