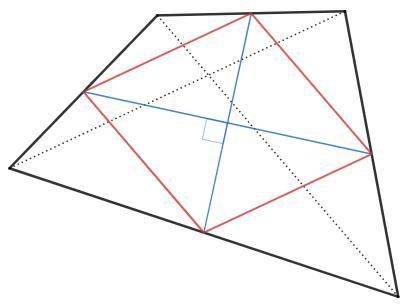
Соединим середины сторон четырехугольника.
Полученные отрезки параллельны диагоналям и равны их половинам, так как являются средними линиями в соответствующих треугольниках.
Отрезки образуют параллелограмм Вариньона.
Площадь четырехугольника Sч =1/2 d₁d₂ sinф
Угол ф между диагоналями четырехугольника равен углу между сторонами пар-ма Вариньона (т.к. они параллельны).
Площадь пар-ма Вариньона Sв =d₁/2 *d₂/2 *sinф =1/2 Sч
Итак, площадь пар-ма Вариньона равна половине площади четырехугольника.
В данном четырехугольнике диагонали равны, следовательно стороны пар-ма Вариньона равны и он является ромбом.
Диагонали ромба перпендикулярны, sin90=1.
Sч =2 Sв =2 *1/2 *14*8 =112
Прямые скрещивающиеся
Прямые непараллельные и непересекающиеся называются скрещивающимися. Один из возможных вариантов чертежа скрещивающихся прямых показан на рис. 4.5, где l m, так как l не параллельна m и l не пересекается с m.
Рис. 4.5
Точка пересечения горизонтальных проекций скрещивающихся прямых является горизонтальной проекцией двух горизонтально конкурирующих точек 1 и 2, принадлежащих прямым l и m. Точка пересечения фронтальных проекций скрещивающихся прямых является фронтальной проекцией двух фронтально конкурирующих точек 3 и 4. По горизонтально конкурирующим точкам 1 и 2 определяется взаимное положение прямых l и m относительно П1. Фронтальная проекция 12 точки 1, принадлежащей прямой l, расположена выше, чем фронтальная проекция 22 точки 2, принадлежащей прямой m (направление взгляда показано стрелкой). Следовательно, прямая l расположена над прямой m.
По фронтально конкурирующим точкам 3 и 4 определяется взаимное положение прямых l и m относительно фронтальной плоскости проекций. Горизонтальная проекция 41точки 4, принадлежащей прямой l, расположена ниже, чем горизонтальная проекция 31 точки 3, принадлежащей прямой m (направление взгляда показано стрелкой). Следовательно, прямая l расположена перед прямой m
V к (конуса)
V ц (цилиндра)
R (радиус цилиндра и конуса)