Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).
Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.
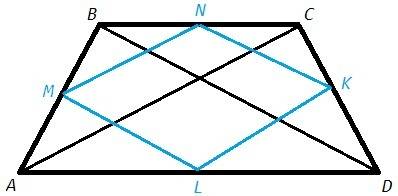
MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.
MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).
AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).
1)
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.⇒
АВ=8 см
СВ²=АВ*ВНСВ=√(8*3)=√24=2√6
АС²=АВ*АН
АС=√(8*5)=2√
2)
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
СН²=АН*ВН
СН=√5*3=√15 см