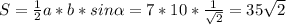 см²
см²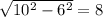 см. Рассмотрим другой прямоугольный треугольник, который сотворен диагональю (гипотенуза), высотой (катет) и вторым катетом, который лежитт на большем основанием трапеции, найдем его:
см. Рассмотрим другой прямоугольный треугольник, который сотворен диагональю (гипотенуза), высотой (катет) и вторым катетом, который лежитт на большем основанием трапеции, найдем его:  см. Найдем большее основание: 6+15=21см, меньшее: 15-6=9см.
см. Найдем большее основание: 6+15=21см, меньшее: 15-6=9см. 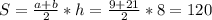 cм².
cм².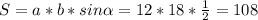 см²
см²
S = √p(p - a)(p - b)(p - c), где p = (a + b + c)/2
p = (5 + 6 + 7)/2 = 18/2 = 9
S = √9(9 - 5)(9 - 6)(9 - 7) = √9•4•3•2 = 3•2√6 = 6√6.
Радиус описанной окружности около треугольника можно найти по формуле:
R = abc/4S
R = 5•6•7/4•6√6 = 35/4√6 = 35√6/24.