У меня получилось что расстояние от точки М до вершины В равно 8 см, показываю как получил:
1. СК и АN - медианы треугольника АВС.
2. По условию задачи точка М удалена от стороны АС на 4 см, то есть она принадлежит перпендикуляру, проведенному к стороне АС.
3. Проведем через эту точку высоту ВН к стороне АС.
4. По условию задачи треугольник АВС равнобедренный, следовательно, высота ВН является еще и медианой.
5. Точка пересечения медиан, согласно их свойствам, делит каждую из них на два отрезка, относящихся как 2 : 1, начиная от вершины, то есть ВМ : НМ = 2 : 1.
ВМ = 4 х 2 = 8 см.
ответ: расстояние от точки М до точки В равно 8 см.
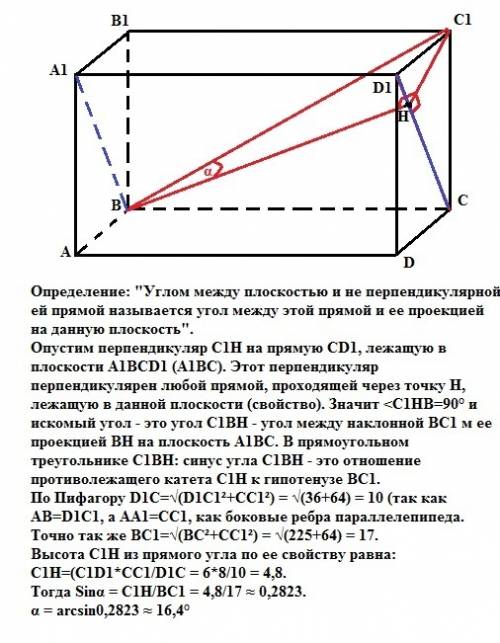
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
В тр-ке АВК ВК²=АВ²-АК²=4-3=1.
Расстояние от точки К до прямой АВ - это высота треугольника АВК. КЕ⊥АВ.
h=ab/c,
КЕ=АК·ВК/АВ=√3·1/2=√3/2 - это ответ.