А₁А₂ = 2 см
Объяснение:
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
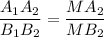
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
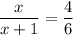
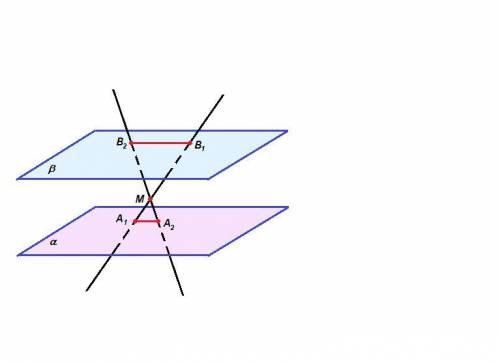
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см
Решение сводится к доказательству равенства АМ и СМ, т.к. сторона ВМ для ∆ АВМ и ∆ СВМ общая.
АВ=СВ (дано) По свойству углов равнобедренного треугольника ∠ВАС=∠ВСА. Примем их равными α. В ∆ ВМС из периметра ВМ+СМ=35-15=20 см
В ∆ АВМ отрезок MN перпендикулярен АВ в её середине. Следовательно, MN- высота и медиана ∆ АВМ, из чего следует ВМ=АМ.
Отрезок МN делит ∆ АВМ на два равных прямоугольных треугольника.
∠ВМА=180°-∠А-∠АВМ=180°-2α.
Угол ВМА - внешний для ∆ ВМС ⇒ посвойству внешнего угла равен двух других, не смежных с ним. ∠В+∠С=180°-2α. В то же время ∠ВМС, смежный углу ВМА, равен 180°-ВМА=180°-(180°-2α), откуда ∠В+∠С=2α. Т.к. ∠С=α, то ∠СВМ=α. Следовательно, ∆ ВСМ равнобедренный, СМ=ВМ=АМ. ⇒ АС=АМ+СМ=ВМ+СМ=20 см