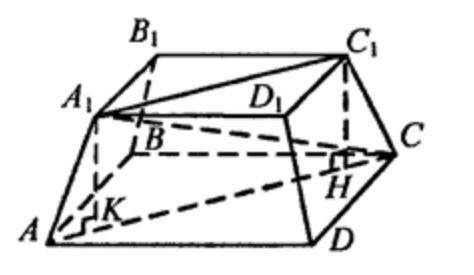
Чтобы построить график такой функции, вам нужно чертить каждую часть отдельно.
1) f(x)= –x–3 , если х ⩽ –3. Это значит, что если х больше –3, то этой функции уже не существует.
f(x)= –x–3 линейная функция. Чтобы нарисовать ее график, достаточно знать пару ее точек.
f(–3)= –(–3)–3=0 — точка (–3; 0).
f(–5)= –(–5)–3=2 — точка (–5; 2).
Соединяете точки и проводите таким образом луч (который имеет начало в точке (–3; 0) и уходит влево). Это красная линия на графике.
2) f(x)= x+3, если –3 < х < 0.
Достаточно знать координаты пары самых крайних точек.
f(–3)= –3+3= 0 — точка (–3; 0)
f(0)= 0+3= 3 — точка (0; 3).
Очевидно, что данные точки не принадлежат графику, так как –3 < х < 0, однако на графике этого не будет видно и будет казаться, что х=3, хотя на самом деле самая крайняя точка будет иметь абсциссу х=–2,999....99.
(Синяя линия на графике)
Так же само рисуете и остальные две части графика.
3) f(x)= –2x+3, если 0 ⩽ х < 3.
Крайние точки:
f(0)= 3 — точка (0; 3)
f(3)= –6+3= –3 — точка (3; –3)
(Зеленая линия на графике)
4) f(x)= 0,5x–4, если х ⩾ 3.
f(3)= 0,5×3–4= 1,5–4= –2,5 — точка (3; –2,5)
f(4)= 0,5×4–4= 2–4= –2 — точка (4; –2)
(Фиолетовая линия на графике)
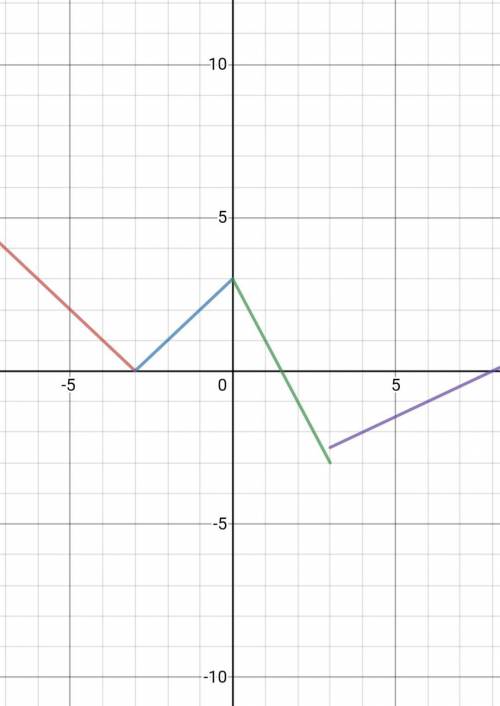
Правильная четырёхугольная пирамида.
Стороны оснований = 5 см, 17 см.
Найти:А1С - ?
Решение:"Правильный многоугольник - многоугольник, у которого все углы и стороны равны".
Так как данная пирамида - правильная, четырёхугольная => основание данной пирамиды - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
НО: Заметим, что нам даны совершенно разные величины оснований пирамиды.
=> перед нами - усечённая правильная четырёхугольная пирамида.
"Усечённая пирамида - часть пирамиды, заключённая между её основанием, боковыми гранями и сечением этой пирамиды".
=> CD = 17 (см), А1В1 = 5 (см).
Итак, у нас два квадрата А1В1С1D1 и АВСD, которые являются основаниями этой усечённый пирамиды.
Диагональным сечение данной усечённой пирамиды является равнобедренная трапеция А1АС1С.
Проведём высоту А1К.
Так как А1С1 и АС - диагонали квадратов АВСD и A1B1C1D1 => A1C1 = A1B1 * √2 = 5 * √2 = 5√2 (см)
Также АС = CD * √2 = 17√2 (см).
А1К ┴ АС, С1Н ┴ АС, так как А1К и С1Н - высоты.
=> А1С1НК - прямоугольник. => А1С1 = КН, А1К = С1Н.
Рассмотрим △АА1К и △СС1Н:
А1К = С1Н, так как А1С1НК - прямоугольник.
АА1 = С1С, так как А1АС1С - равнобедренная трапеция.
=> △АА1К = △СС1Н, по карету и гипотенузе.
=> АК = СН = 1/2(АС - А1С1) = 1/2(17√2 - 5√2) = 6√2 (см)
=> СК = АС - АК = 17√2 - 6√2 = 11√2 (см)
Найдём А1С, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
√(4² + (11√2)²) = √(16 + 121 * 2) = √258 (см)
ответ: √258 (см)