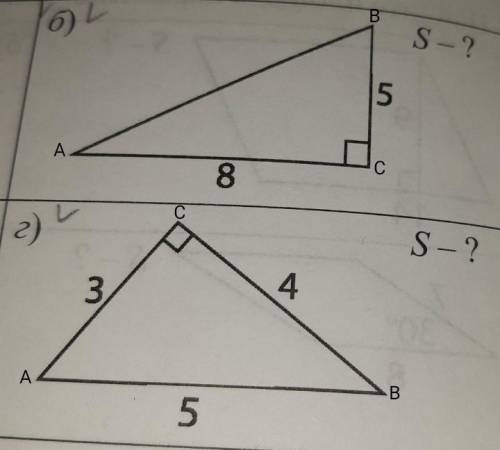
б) S = ½×8 (ед)×5 (ед) = 20 (ед²).
По теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы) найдём гипотенузу АВ —
АВ² = АС² + ВС² = 8² + 5² = 64 + 25 = 89⇒АС = √89.
Найдём тангенс ∠А (отношение противолежащего катета к прилежащему) —
tg(∠A) = BC/AC = 5/8 = 0,625.
В таблице Брадиса тангенсов это примерное значение тангенса острого угла в 32°.
Тогда второй острый угол ∆АВС по теореме о сумме острых углов прямоугольного треугольника —∠В = 90° - ∠А ≈ 90° - 32° ≈ 58°.
г) S = ½×3 (ед)×4 (ед) = 6 (ед²).
Найдём тангенс ∠А —
tg(∠А) = CB/AC = 4/3 ≈ 1,3.
В таблице Брадиса тангенсов это примерное значение тангенса острого угла в 53°.
Найдём ∠В —
∠В = 90° - ∠А ≈ 90° - 53° ≈ 37°.
на первой картинке угол А равен 30°, а катет лежащий против угла в 30° равен половине гипотенузы. то есть мы должны 4•2=8 ответ
на второй картинке все анологично.угол В равен 60° значит угол А= 180-90-60= 30°
опять теорема катет лежащий против угла в 30° равен половине гипотенузы. теперь гипотенуза у нас АВ значит 10:2=5 ответ
на третьей картинке рассмотрим треугольник АВС самый большой. видим что угол В=45°, следовательно и угол А будет равен так же: 180-90-45=45°
углы мы нашли, теперь рассмотрим прямую ДС- она обозначана квадратиком, то есть 90° . значит это высота. это тема расстояние от точки до прямой, кароче говоря 8•2=16 это ответ
Тогда столб и тень образуют прямоугольный треугольник KMN
ABC подобен KMN, т.к. подобны две стороны и угол между ними (столб и труба вертикальны, тени горизонтальны, угол = 90 градусов)
составим пропорцию
длина трубы (х) / длина тени (37,6) = длина столба (3,8) / дл.тени(3,04)
3,04х=37,6*3,8
х=47
ответ: 47м