ответ: ФТЛ? ДКР?
Объяснение:
#include <iostream>
using namespace std;
int main() {
int a, b, c;
cin >> a >> b >> c;
if (a == b && a == c && b == c) {
cout << 3;
}
if (a == b && a != c && b != c) {
cout << 2;
}
if (a != b && a == c && b != c) {
cout << 2;
}
if (a != b && a != c && b == c) {
cout << 2;
}
if (a != b && a != c && b != c) {
cout << 0;
}
return 0;
}
а вообще, я сам не знаю как эту задачу решить... Т_Т
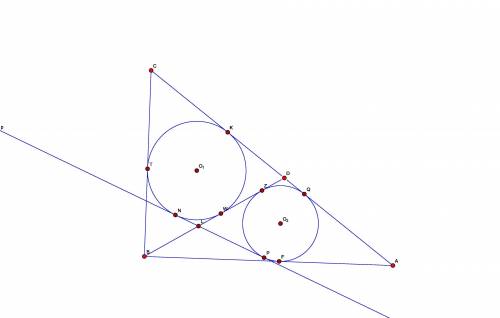
1) Я долго сомневался, как лучше сделать, и все-таки решил не выводить здесь известные свойства внешних и внутренних касательных к двум окружностям. Просто перечислю то, что нужно знать для решения этой задачи. Найдите в учебниках или докажите сами.
LD = NP = KQ;
кроме того, равны и "кусочки" этих отрезков:
LN = LW = DZ = DQ; DK = DW = LZ = LP;
(некоторые, я в том числе, испытывают серьезные трудности восприятия этих равенств, когда впервые с ними сталкиваются, особенно с учетом того, как просто они получаются)
2) BZ = BF = BL + LZ = BL + DK; аналогично BT = BW = BL + DQ;
=> BL + DK + BL + DQ + CT + AF + AC = 2p; (как всегда, p - полупериметр ABC)
CT + AF = AC - QK;
=> 2*BL + QK + 2*AC - QK = 2p;
=> BL = p - AC = (AB + BC - AC)/2 = 2; это в точности равно радиусу вписанной в ABC окружности.
S = AB*BC*0.5 = 36/2 = 18 см².
V = Sh = S*AA₁ = 72 см³.