Вкубе a…d1 найдите косинус угла между ребром a1d1 и плоскостью решить подробно, обязательно с чертежом, если вы не хотите делать чертеж, то , не приступайте к решению.

👇

Ответ:

МаринаБалыгина505212

22.09.2022

АВ1, В1Д1 и АД1 - диагонали граней куба, значит они равны. ΔАВ1Д1 - правильный.
АА1=А1В1=А1Д, значит пирамида А1АВ1Д1 - прямая, основание высоты которой лежит в точке пересечения биссектрис.
Д1К - биссектриса и высота тр-ка АВ1Д1.
АВ1=а√2, где а - ребро куба.
Д1К=АВ1√3/2=а√2·√3/2=а√6/2.
А1К⊥А1Д1.
В прямоугольном тр-ке А1Д1К cos∠А1Д1К=А1Д1/Д1К=а·2/а√6=√6/3 - это ответ.
Вкубе a…d1 найдите косинус угла между ребром a1d1 и плоскостью решить подробно, обязательно с чертеж

Вкубе a…d1 найдите косинус угла между ребром a1d1 и плоскостью решить подробно, обязательно с чертеж

4,8(85 оценок)

Открыть все ответы

Ответ:

роза266

22.09.2022

AB =16 ; ∠A =30° ; ∠B =105° .

1) BC -?
2) (меньшая сторона) -?

1) AB/sin∠C =BC/sinA = AC/sin∠B = 2R (теорема синусов).
∠C =180° -(∠A +∠B )= 180° -(30° +105°) =45°.
16/sin45° =BC/sin30°⇒
BC =15*(sin30°/sin45°) =16*(1/2) / (1/√2) =(16√2)/2 =8√2≈11,28 (см).
---
2) меньшая сторона та, которая лежит против меньшего угла ,
эта сторона BC(лежит против меньшего угла ∠A=30°).

длину  AC не требуется , но :
AC /sin∠B = AB/sin∠C ⇒AC =AB*sin(∠B)/(sin∠C)=
16* sin105°/(1/√2) =16√2sin105°=16√2*√2(√3 +1)/4 =8(√3 +1) .

sin105° =sin(180°-75°) =sin75°=sin(45°+30°) =...
или
sin105° =sin(60°+45°) =sin60°*cos45°+cos60°*sin45°=
(√3/2)*(√2/2)+(1/2)*(√2/2) =√2(√3 +1)/4.

* * * * * * * Второй
∠C =180° -(∠A+∠B) =180° -(30°+105°) =45°.
Проведем высоту BH⊥AC (∠AHB=90°) ⇒ Прямоугольный треугольник BHC  равнобедренный CH =BH ,т.к. ∠C =45°.
По теореме Пифагора из ΔBHC:
BC =√ (BH² +CH²) =√(2BH²) =BH√2 . Но из ΔABH BH=AB/2 =8(как катет против угла
∠A =30°). Значит BC =BH√2 =8√2.

4,7(4 оценок)

Ответ:

Сэээээ

22.09.2022

1) Точка, лежащая на единичной окружности имеет абсциссу, равную косинусу соответствующего угла, а ординату , равную синусу этого угла.

То есть, если точка А лежит на единичной окружности, то её координаты можно записать так: $A(\, cosa\, ;\, sina\, )$ .

Основное тригонометрическое тождество имеет вид: 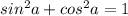sin^2a+cos^2a=1 .

Поэтому проверяем это тождество для заданных координат.

$A\Big(\, \dfrac{1}{2}\, ;-\dfrac{1}{2}\, \Big):\ \ \Big(\dfrac{1}{2}\Big)^2+\Big(-\dfrac{1}{2}\Big)^2=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\ne 1\\\\\\B\Big(\dfrac{\sqrt3}{2}\, ;-\dfrac{1}{2}\, \Big):\ \ \Big(\dfrac{\sqrt3}{2}\Big)^2+\Big(-\dfrac{1}{2}\Big)^2=\dfrac{3}{4}+\dfrac{1}{4}=1\ \ \to \ \ B\in okryznosti\\\\\\C\Big(-\dfrac{\sqrt3}{4}\, ;\, \dfrac{1}{4}\, \Big):\ \ \Big(-\dfrac{\sqrt3}{4}\Big)^2+\Big(\dfrac{1}{4}\Big)^2=\dfrac{3}{16}+\dfrac{1}{16}=\dfrac{1}{4}\ne 1$

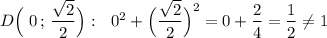
$D\Big(\; 0\, ;\, \dfrac{\sqrt2}{2}\Big):\ \ 0^2+\Big(\dfrac{\sqrt2}{2}\Big)^2=0+\dfrac{2}{4}=\dfrac{1}{2}\ne 1$

На единичной окружности лежит точка 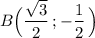$B\Big(\dfrac{\sqrt3}{2}\, ;-\dfrac{1}{2}\, \Big)$ .

Найдём значение угла, соответствующего точке В, лежащей на единичной окружности.

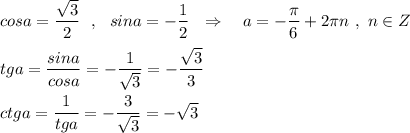
$cosa=\dfrac{\sqrt3}{2}\ \ ,\ \ sina=-\dfrac{1}{2}\ \ \Rightarrow \ \ \ a=-\dfrac{\pi}{6}+2\pi n\ ,\ n\in Z\\\\tga=\dfrac{sina}{cosa}=-\dfrac{1}{\sqrt3}=-\dfrac{\sqrt3}{3} \\\\ctga=\dfrac{1}{tga}=-\dfrac{3}{\sqrt3}=-\sqrt3$

Смотри рисунок.

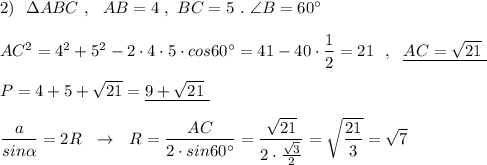
$2)\ \ \Delta ABC\ ,\ \ AB=4\ ,\ BC=5\ .\ \angle B=60^\circ \\\\AC^2=4^2+5^2-2\cdot 4\cdot 5\cdot cos60^\circ =41-40\cdot \dfrac{1}{2}=21\ \ ,\ \ \underline {AC=\sqrt{21}\ }\\\\P=4+5+\sqrt{21}=\underline {9+\sqrt{21}\ }\\\\\dfrac{a}{sin\alpha }=2R\ \ \to \ \ R=\dfrac{AC}{2\cdot sin60^\circ }=\dfrac{\sqrt{21}}{2\cdot \frac{\sqrt3}{2}}=\sqrt{\dfrac{21}{3} }=\sqrt7$

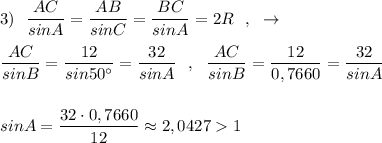
$3)\ \ \dfrac{AC}{sinA}=\dfrac{AB}{sinC}=\dfrac{BC}{sinA}=2R\ \ ,\ \ \to \\\\\dfrac{AC}{sinB}=\dfrac{12}{sin50^\circ }=\dfrac{32}{sinA}\ \ ,\ \ \dfrac{AC}{sinB}=\dfrac{12}{0,7660}=\dfrac{32}{sinA}\\\\\\sinA=\dfrac{32\cdot 0,7660}{12}\approx 2,04271$

Так как sin любого угла не превосходит 1, то полученный результат говорит о том, что треугольника с такими размерами не существует. Решения задача не имеет .

4,8(45 оценок)

Это интересно:

Семейная-жизнь

28.05.2021

Как помочь родителям, которые похоронили своего ребенка: советы и рекомендации...

Компьютеры-и-электроника

26.03.2023

Как изменить проверочный номер для кода безопасности iCloud на iPhone...

Здоровье

02.09.2020

Польза и способы приема пчелиной пыльцы...

Компьютеры-и-электроника