В плоскости α проведем В₁Н⊥АС. В₁Н - проекция ВН на плоскость α, значит ВН⊥АС по теореме о трех перпендикулярах. Значит
∠ВНВ₁ = 45° - линейный угол двугранного угла ВАСВ₁;
ВН - высота треугольника АВС, искомое расстояние от точки В до прямой АС.
∠ВАН = 180° - ∠ВАС = 180° - 150° = 30° по свойству смежных углов.
В прямоугольном треугольнике АВН, ВН = 1/2 АВ = 1 см по свойству катета, лежащего напротив угла в 30°.
Итак, расстояние от точки В до прямой АС
ВН = 1 см.
ВВ₁ - расстояние от точки В до плоскости α.
ΔВВ₁Н: ∠ВВ₁Н = 90°
ВВ₁ = ВН · sin45° = 1 · √2/2 = √2/2 см
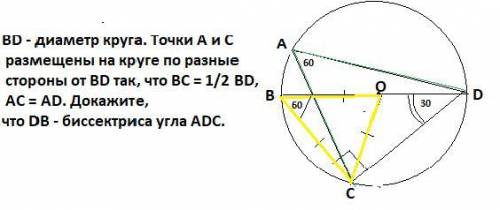
BD - диаметр круга. Точки А и C размещены на круге по разные стороны от BD так, что BC = 1/2 BD, AC = AD. Докажите, что DB - биссектриса ∠ADC.
Объяснение:
1) Т.к. BC= 1/2*BD=ВО ,и ВО=ОС как радиусы , то ΔВОС -равносторонний ⇒∠СВD=180°:3=60°.
2) На дугу СD опираются два вписанных угла ⇒ по свойству вписанных углов ∠CBD=∠CAD=60°
2)Точки C размещена на окружности ⇒∠ВСD=90° , тк опирается на диаметр BD. Значит ∠ВDС=90°-60°=30°.
3) Т.к. AC=AD ,то ΔCAD-равнобедренный ⇒∠АСD=∠ADС=(180°-60°):2=60°. Поэтому на частичку угла ∠ADB=60°-30°=30°
4) Получили ∠ADB=30°( п 3)
∠ВDС=30°( п 2)⇒ DB - биссектриса ∠ADC.