Объяснение:
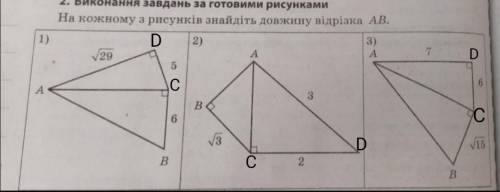
1)
∆ADC- прямоугольный.
По теореме Пифагора найдем гипотенузу
АС=√(AD²+DC²)=√(29+25)=√54.
∆ACB- прямоугольный.
По теореме Пифагора найдем гипотенузу
АВ=√(АС²+СВ²)=√(54+36)=√90=3√10
ответ: АВ=3√10
2)
∆АСD- прямоугольный.
По теореме Пифагора найдем катет
АС=√(AD²-CD²)=√(3²-2²)=√(9-4)=√5
∆ABC- прямоугольный.
По теореме Пифагора найдем катет
АВ=√(АС²-ВС²)=√(5-3)=√2
ответ: АВ=√2
3)
∆ADC- прямоугольный.
По теореме Пифагора найдем гипотенузу.
АС=√(АD²+DC²)=√(7²+6²)=√(49+36)=√85
∆ACB- прямоугольный.
По теореме Пифагора найдем гипотенузу
АВ=√(АС²+СВ²)=√(85+15)=√100=10
ответ: АВ=10
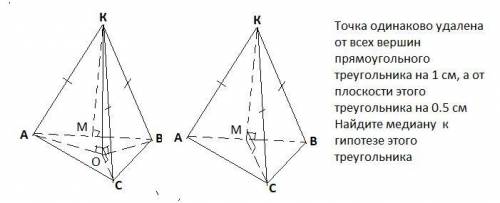
Точка одинаково удалена от всех вершин прямоугольного треугольника на 1 см, а от плоскости этого треугольника на 0.5 см найдите медиану гипотезе этого треугольника
Объяснение:
1.Пусть КМ-медиана ΔAКB - равнобедренный, поэтому КM ⊥ AB по свойству медианы равнобедренного треугольника.
Пусть в ΔКCM проведем КO⊥ СМ. Тогда ОА=ОВ=ОС как проекции равных наклонных равный наклонные, поэтому ОА = ОВ= ОС = R, R - радиус описанной окружности около ΔАВС. Но центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы , поэтому точки М и О совпадают. ⇒
КM ⊥ ( АВС).
2)Т.к. М-середина АВ , то СМ-медиана к гипотенузе ΔАВС.
ΔАКМ-прямоугольный, АК=1 см, КМ=0,5 см, по т. Пифагора АМ=√(1²-0,5²)=√0,75=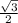 
( см).
R=АМ=ВМ=СМ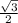, СМ= см
В треугольнике против большей стороны лежит больший угол.
Доказательство:
Пусть в ΔАВС АВ > ВС. Докажем, что ∠С > ∠А.
Отложим на стороне АВ отрезок ВК = ВС. Так как АВ > ВС, то точка К будет лежать между точками А и В, тогда угол 1 будет частью угла С:
∠1 < ∠С.
∠2 - внешний для ΔАСК, а внешний угол треугольника равен сумме двух внутренних, не смежных с ним. Тогда ∠2 = ∠А + ∠АСК, т.е.
∠2 > ∠А.
И еще ∠1 = ∠2 как углы при основании равнобедренного треугольника ВСК. Получаем:
∠А < ∠2 < ∠C, значит
∠А < ∠С
Обратная теорема: В треугольнике против большего угла лежит большая сторона.
Доказательство:
Пусть в треугольнике АВС ∠С > ∠A. Докажем, что АВ > ВС.
Предположим, что АВ < ВС. Тогда по доказанной теореме ∠С должен быть меньше ∠А. Это противоречит условию. Значит предположение неверно, АВ > ВС.