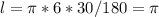
б) На сторонах СD и DE треугольника CDE отметили точки K и L так,что CK:KD=EL:LD =2/3 . Докажите что треугольники CDE и KDL подобны. Найдите коэффициент подобия.
ответ: 5/3
Объяснение: б ) CK/KD =EL/ LD = 2 /3 +1 =5/3 .
CK/KD+ 1 = EL/ LD +1 =2 /3 +1 ⇔ (CK+KD) /KD = (EL+ LD)/ LD =(2+3)/3⇔ DC/KD= DE/LD = 5/3
∠В - общий
Следовательно Δ CDE ~ Δ KDE ( второй признак подобия )
k = 5/3 коэффициент подобия.
* * * P.S. Для подобия достаточно условие CK/KD =EL/ LD * * *
ответ: Угол AOD равен 135 градусам;
Угол AOB равен 165 градусов.
Пошаговое объяснение:
Первым действием мы найдем угол AOD: В задаче сказано что угол AOD равен 75% от РАЗВЕРНУТОГО угла. А сколько градусов в развернутом углу?(180) 180*0,75=135(г.)-угол AOD
Далее в задаче говорится что угол AOD равен девяти одиннадцатым угла BOC: 135:9*11=165(г.)-угол BOC.
Оформление(как нужно переписать в тетрадь):
1)180*0,75=135(г.)-угол AOD
2)135:9*11=165(г.)-угол BOC
ответ: AOD=135 градусов
BOC=165 градусов
Нарисовать я надеюсь вы сами сможете)