1) ≈71,05
Объяснение:
1) В основании у нас получается равнобедренный треугольник(две стороны - радиус одной окружности) с углом в 90° в центре окружности и высотой 2см. Т.к. треугольник равнобедренный, следует высота=биссектрисе.
Находим радиус окружности:
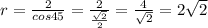см
Находим высоту цилиндра:
Т.к. проведенное пересечение у нас квадрат, следует высота цилиндра равна основанию треугольника(в основании цилиндра)
Половина основания треугольника(она же половина высоты) равна
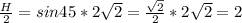см
Следует высота равна
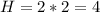см
Находим площадь боковой поверхности цилиндра:
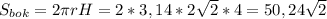≈71,05
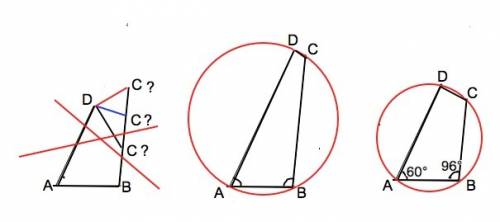
Задача имеет решение только если АВСD – четырехугольник, вписанный в окружность. (см. рисунки вложения)
В противном случае величину углов АDC и DCB вычислить невозможно, они могут принимать различное значения, лишь бы их сумма была равна разности между суммой углов четырехугольника и суммой углов АВС и BAD, т.е. 204°
-----------
Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º.
Тогда ∠ADC=180°-∠ABC=180°-96=84°
∠BCD=180°-∠BAD=180°-60°=120°⇒
∠BCD-∠ADC=120°-84°=36°.
