1. Отрезки касательных, проведенных из одной точки, равны, значит
ВА = ВС.
Радиус, проведенный в точку касания, перпендикулярен касательной, значит
ОА⊥ВА и ОС⊥ВС.
ΔОВА = ΔОВС по гипотенузе и катету (ВО - общая, ВА = ВС), значит ВО - биссектриса угла АВС.
∠ОВА = 1/2∠АВС = 30°, тогда в прямоугольном треугольнике ОВА против угла в 30° лежит катет, равный половине гипотенузы:
ОА = 1/2 ОВ = 1/2 · 28 = 14
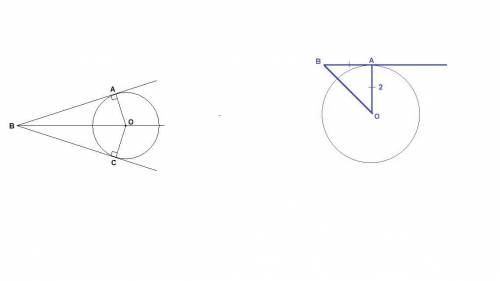
2. Радиус, проведенный в точку касания, перпендикулярен касательной.
Значит ΔАОВ прямоугольный и равнобедренный (АВ = ОА = 2 см). По теореме Пифагора:
ОВ = √(АВ² + ОА²) = √(4 + 4) = 2√2 см
Найти все углы
Решение:<1 и <3-вертикальные при a//b и с-секущей=> <1=<3=102
<2 и <4 -вертикальные при a//b и с-секущей=><2=<4=102
<1 и <5- смежные при a//b и с-секущей=><1+<5=180 =><5=180-<1=180-102=78
<5 и <6-вертикальные при a//b и с-секущей=><5=<6=78
<6 и <8-сooтветственные при a//b и с-секущей=>пo II свoйству параллельных прямых <6=<8=78
<8 и <7-вертикальные при a//b и с-секущей=><8=<7=78
Oтвет:<3=102,<4=102,<5=78,<6=78<7=78,<8=78