а) Площадь сектора 6π см² , дуга сектора 2π см
Формула площади сектора через длину дуги
S=L•R/2
6π=2πR/2⇒
R=6
б)
Длина дуги сектора равна длине дуги в 1°, умноженной на величину угла сектора.
L=(2πR:360°)•n , где n - угол сектора
2π=2πR:360•n ⇒
n=2π •360:12π=60°
в)
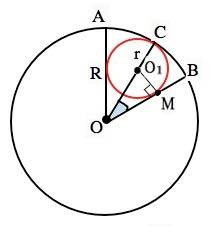
Рассмотрим чертеж приложения, в котором угол сектора АОВ=60°, С -точка касания окружностей, О1 - центр вписанной в сектор АОВ окружности. Он лежит на ОС, биссектрисе угла АОВ.
АО=ОВ=ОС=6
Проведем из О1 радиус в точку касания М вписанной окружности с ОВ.
Треугольник ОО1М прямоугольный, ∠О1ОМ=30°, ОО1 - гипотенуза, О1М - катет= r
ОО1=ОС - О1С=6-r
r противолежит углу 30°⇒
r=(6-r):2 ⇒
3r=6 см
r=2 см