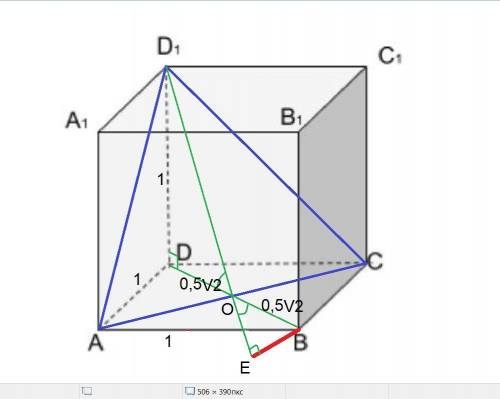
Пусть дана плоскость ACD1 в виде линий пересечения её с гранями куба.
Действия:
1) Проводим диагональ DB основания.
Этим самым мы находим точку О, через которую проходит плоскость, перпендикулярная к заданной.
2) Проводим прямую D1O.
Эта прямая - линия пересечения заданной плоскости и плоскости, перпендикулярной к ней.
3) Проводим отрезок ВЕ, перпендикулярный к D1O.
Задание выполнено.
Желающие могут определить фактическую длину такого перпендикуляра по заданным размерам куба.
Примем длину ребра куба, равную а, длину перпендикуляра - х.
Половина диагонали основания равна а√2/2.
Длина отрезка D1O равна:
D1O = √(а² + (а√2/2)²) = √(а² + 2а²/4) = √(6а²/4) = а√3/√2.
Из подобия треугольников составляем пропорцию.
x/(а√2/2) = a/а√3/√2.
Отсюда х = а√3/3.
Объяснение:
В - 2 .
1 . PK = AB = CD - як сторони ромбів зі спільною стороною АВ .
PK║AB , AB║CD - властивістю ромбів як паралелограмів . За
транзитивною властивістю паралельності прямих у просторі PK║CD .
А 4 - кутник PKCD , у якого дві протилежні сторони паралельні і
рівні , є паралелограмом . Доведено .
2 . Проведемо АС║А₁В₁ ; ММ₁ ∩ АС = { N } . ВС = ВВ₁ - АА₁ =
= 16 - 10 = 6 ( см ) ; вс = 6 см .
ММ₁║ВВ₁ , тому ΔАMN ∼ ΔABC . Тому MN/BC = AM/AB ; звідси
MN = ( BC * AM )/AB = ( 6 * 2k )/3k = 12/3 = 4 ( см ) ; MN = 4 см .
Тоді шуканий відрізок ММ₁ = MN + NM₁ = MN + AA₁ = 4 + 10 = 14 ( см ) ;
ММ₁ = 14 см .
2) Проведем высоту трапеции. Получим прямоугольный треугольник, в котором высота трапеции является катетом, лежащим против угла 30 гр и рана половине гипотенузы, т.е. боковой стороне трапеции:
4*1/2 = 2(см)
3) 22*2/2 = 22 см^2 площадь трапеции
2. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований, или ее средней линии. Значит, площадь данной трапеции равна:
S = 18/2 * 18/2 = 81 см^2.