Не достатньо даних.
Объяснение:
BH- висота, медіана і бісектриса рівнобедреного трикутника ∆АВС, АВ=ВС, за умови.
АН=СН, ВН- медіана.
АН=АС/2=24/2=12см
∆АВН- прямокутний трикутник.
За теоремою Піфагора:
ВН=√(АВ²-АН²=√(18²-12²)=
=√((18-12)(18+12))=√(6*30)=
=√(2*3*2*3*5)=6√5 см.
ВН перпендикулярно АС, тоді МН перпендикулярно АС, за теоремою о трьох перпендикулярах. Необхідно знайти МН.
Далі не стає даних.
Пояснення
∆ВМН- прямокутний трикутник.
За теоремою Піфагора:
МН²=ВМ²+ВН².
Візьмемо за ВМ=х.
МН=√(х²+(6√5)²)=√(х²+180)

Периметр четырехугольника АСЕК равен 54 ед.
Объяснение:
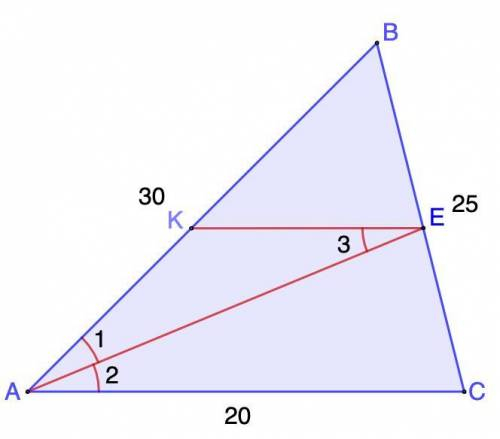
В треугольнике ABC, AB = 30, AC = 20, BC = 25; AE - биссектриса угла A. Из точки E проведена параллельная прямая к стороне AC, которая пересекает сторону AB в точке K. Найдите периметр четырехугольника ACEK.
Дано: ΔАВС;
AB = 30, AC = 20, BC = 25;
AE - биссектриса;
ЕК || AC.
Найти: Р(АСЕК)
1. AE - биссектриса;
Свойство биссектрисы:
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.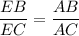
Пусть ЕВ = х, тогда ЕС = 25 - х
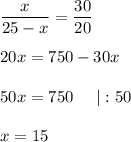
⇒ EB = 15; EC = 10.
2. Рассмотрим ΔКВЕ и ΔАВС.
Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.⇒ ΔКВЕ ~ ΔАВС
Запишем отношения сходственных сторон:
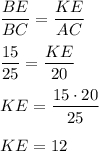
3. Рассмотрим ΔАКЕ.
∠1 = ∠2 (условие)
∠3 = ∠2 (накрест лежащие при КЕ || AC и секущей АЕ)
⇒ ∠1 = ∠3
Если в треугольнике два угла равны, то он равнобедренный.⇒ АК = КЕ = 12
4. Рассмотрим АСЕК.
Периметр - сумма длин всех сторон.Р(АСЕК) = АК + КЕ + ЕС + АС = 12 + 12 + 10 + 20 = 54
Периметр четырехугольника АСЕК равен 54 ед.
Пусть a:b:c=3:5:6=3x:5x:6x.
(4√30)²=9х²+25х²+36х²,
70х²=480,
х²=48/7,
х=4√3/√7=4√21/7.
а=3х=12√21/7,
b=5x=20√21/7,
c=6x=24√21/7.