АВ/MN = BC/M=2 угол В= углу N , следовательно ABC подобен MNK
составим пропорцию: 12/6 = х/7 АС = 12*7/6 = 14;
угол K = углу С (т к в подобных теугольниках углы равны) следовательно угол С = 60
Есть пирамида АВСДА1В1С1Д1, где АВСД - нижнее основание, О - центр нижнего основания, т.Л - середина стороны СД. Аналогично назовем Л1 и О1 для верхнего основания А1В1С1Д1. Восстановим вершину усеченной пирамиды и назовем ее т.К.
Рассмотрим прямоугольный треугольник КЛО: т.к. КО - катет, лежащий против угла КЛО=30 градусов, то КЛ=2*КО. ОЛ=АД/2=24/2=12. Примем КО за х. Тогда КО^2+ОЛ^2=КЛ^2; х^2+12^2=(2х)^2; х=КО=4*корень из 3; КЛ=8*корень из 3.
Из подобия треугольников КЛО и КЛ1О1:
ОЛ/О1Л1=КО/КО1, отсюда КО1=О1Л1*КО/ОЛ=(20/2)*(4*корень из 3)/12=10/корень из 3
V усеч. = V(КАВСД) - V(КА1В1С1Д1)=S(АВСД)*КО/3- S(А1В1С1Д1)*КО1/3=
=24*24*4*(корень из 3)/3-20*20*(10/корень из 3)/3=2912/(3*корень из 3)
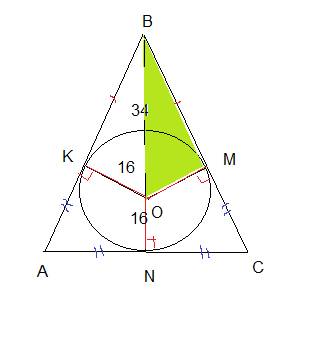
к=(АВ:МN)=(ВС:NK)=(12:6)=(18:9)=2 =>треуг.АВС˷MNK-по 2 признаку подобия треугольков=>
˻С=˻К=60
АС=МК*к=7*2=14см
ответ:АС=14см, ˻С=60