Например стороны треугольника АB=6 cm, BC=8cm - это катеты, надо найти BC - гипотенузу.
По теореме Пифагора:
BC^2=AB^2+BC^2;
BC^2=36+64;
BC^2=100;
BC=10(cm);
Площадь прямоугольного треугольника по двум катетам:
S=a*b/2
S=AB*BC/2
S=8*6/2=24cm^2
Мага́дха (санскр. मगध) — древняя страна и историческая область в Индии, упоминаемая ещё в Рамаяне и Махабхарате, управлялась царями-буддистами. За долгую историю Индии сменялось множество династий Магадхи (Шайшунага, Нанда и др.). Магадха входила в список шестнадцати махаджанапад — больших государств в буддийских и джайнских источниках. Царь Бимбисара (543—491 до н. э.) из династии Харьянка, живший во времена Будды развитию буддизма и хорошо относился к джайнизму.
Образование Магадхи, по сведению в ведических текстах, произошло около 600 года до н. э. Самое раннее упоминание Магадхи происходит в Атхарваведе, где они перечисляются наряду с ангами, гандхари и муджаватами. Ядром королевства была область Бихара к югу от Ганга; его первой столицей была Раджагриха (современный Раджгир), затем Паталипутра (современная Патна). Магадха расширилась, когда была присоединена большая часть Бихара и Бенгалии с завоеванием Конфедерации Ваджжи и Анги. В конечном итоге королевство Магадха охватило Бихар, Джаркханд, Ориссу, Западную Бенгалию, восточный Уттар-Прадеш и районы современных Бангладеш и Непала.
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
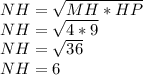
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
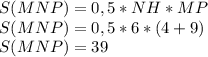
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
по теореме пифагора находим:
6²+8²= 10²
значит, гипотенуза равна 10 см
S пр. треуг= аб/2 , где а и б - стороны
S=6*8/2 = 24 см²