<ADB = 40°
Объяснение:
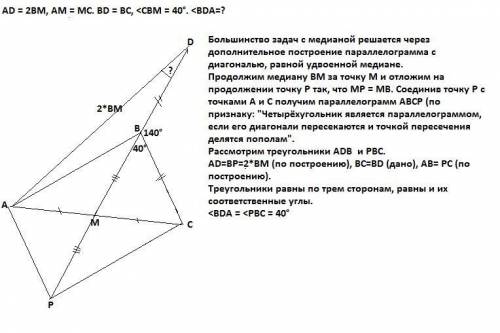
Большинство задач с медианой решается через дополнительное построение параллелограмма с диагональю, равной удвоенной медиане.
Продолжим медиану ВМ за точку М и отложим на продолжении точку Р так, что МР = МВ. Соединив точку Р с точками А и С получим параллелограмм АВСР (по признаку: "Четырёхугольник является параллелограммом, если его диагонали пересекаются и точкой пересечения делятся пополам".
Рассмотрим треугольники ADB и РВС.
AD=BP=2*BM (по построению), BC=BD (дано), АВ= РС (по построению).
Треугольники равны по трем сторонам, равны и их соответственные углы. <BDA = <PBC = 40°.
Соединим вершины В и D четырехугольника.
Треугольники ВАD и CBD - равнобедренные, углы каждого при их общем основании BD равны, следовательно, равны и суммы этих углов. ∠АВС=∠ АDС.
Сумма внутренних углов выпуклого четырехугольника 360°;
∠АВС+∠АDС=360°-(∠АВС+∠ АDС)
∠АВС+∠АDС=360°-180°=180°
Тогда ∠В=∠D=180°:2=90°