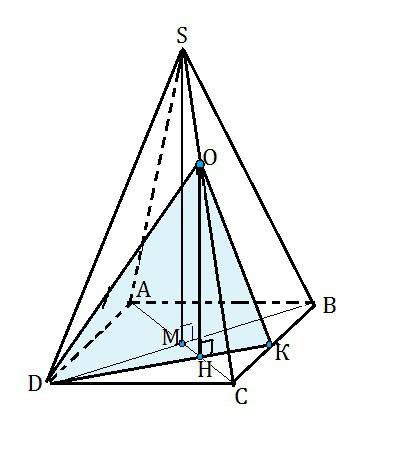
SABCD -правильная четырехугольная пирамида. Постройте сечение пирамиды плоскостью, проходящей через DO (точка О-внутренняя точка отрезка SC) и перпендикулярной плоскости ABC.
Если искомая площадь перпендикулярна плоскости АВС, то она перпендикулярна плоскости АВСD.
Проведем диагональное сечение АSС пирамиды .
О лежит на ребре SC и принадлежит этому диагональному сечению.
Опустим в плоскости ∆ ASC из О перпендикуляр ОН на АС (он лежит в плоскости диагонального сечения, перпендикулярной основанию, параллелен высоте пирамиды, и потому перпендикулярен её основанию).
Через D и Н проведем прямую до пересечения с ВС в точке К.
Соединим D, О и К.
Через 3 точки можно провести плоскость, притом только одну.
Плоскость ∆ DОК - сечение пирамиды.
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Плоскость ∆ DОК проходит через ОН, перпендикулярный плоскости основания, и является искомым сечением
∠BOK = 46°
Объяснение:
Смотри прикреплённый рисунок.
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности, поэтому
∠ОВК = 0,5 ∠ КВМ = 0,5 · 88° = 44°.
ΔВОК - прямоугольный (∠ВКО = 90°, так как касательная ВК перпендикулярна радиусу ОК).
Сумма острых углов прямоугольного треугольника равна 90°
∠ВОК + ∠ОВК = 90°
∠ВОК = 90° - ∠ОВК = 90° - 44° = 46°