5 дм.
Объяснение:
Проведем DM ⊥ BC.
Тогда по теореме о трех перпендикулярах КМ ⊥ ВС и будет являться расстоянием от точки К до катета ВС .
По условию ΔАВС - прямоугольный. Тогда ∠ АСВ= 90°, ∠DMC =90° по построению . Значит, DM ║AC и проходит через середину. Тогда точка М - середина катета ВС и отрезок DM является средней линией ΔАВС.
Средняя линия треугольника параллельна стороне и равна ее половине.
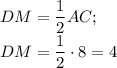
Тогда DM= 4 дм
Так как DК перпендикуляр к плоскости ΔАВС, то он перпендикулярен любой прямой, лежащей в этой плоскости.
Значит, DК⊥ DМ и Δ DМК - прямоугольный.
Найдем КМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
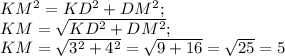
Значит, KM= 5 дм - искомое расстояние
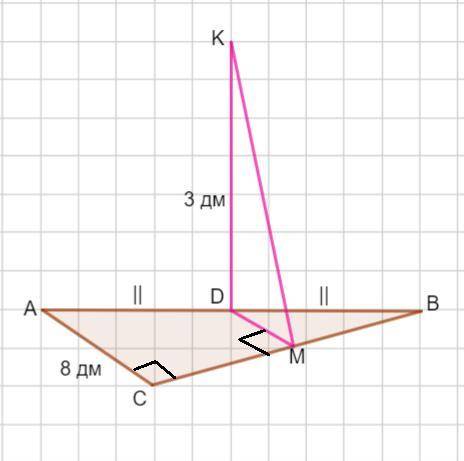
Проведем DM ⊥ BC.
Тогда по теореме о трех перпендикулярах КМ ⊥ ВС и будет являться расстоянием от точки К до катета ВС .
По условию ΔАВС - прямоугольный. Тогда ∠ АСВ= 90°, ∠DMC =90° по построению . Значит, DM ║AC и проходит через середину. Тогда точка М - середина катета ВС и отрезок DM является средней линией ΔАВС.
Средняя линия треугольника параллельна стороне и равна ее половине.
\begin{gathered}DM=\dfrac{1}{2} AC;\\DM=\dfrac{1}{2} \cdot 8=4\end{gathered}DM=21AC;DM=21⋅8=4
Тогда DM= 4 дм
Так как DК перпендикуляр к плоскости ΔАВС, то он перпендикулярен любой прямой, лежащей в этой плоскости.
Значит, DК⊥ DМ и Δ DМК - прямоугольный.
Найдем КМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
\begin{gathered}KM^{2} =KD^{2} +DM^{2}; \\KM= \sqrt{KD^{2} +DM^{2}} ;\\KM= \sqrt{3^{2} +4^{2} } =\sqrt{9+16} =\sqrt{25} =5\end{gathered}
5 дм