Дано:
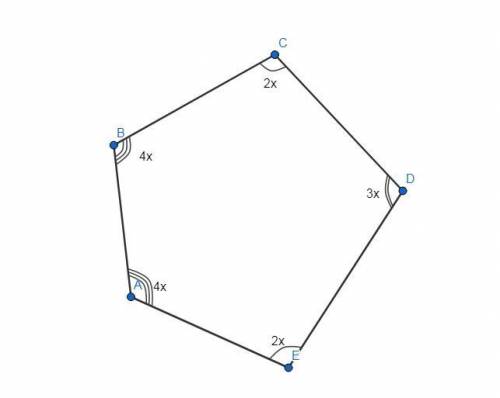
ABCDE - выпуклый пятиугольник.
∠A : ∠В : ∠С : ∠D : ∠E = 4 : 4 : 2 : 3 : 2.
Найти:
∠A, ∠В, ∠С, ∠D, ∠E = ?
Сумма углов выпуклого n-угольника вычисляется по формуле -
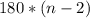
Где n - количество сторон.
Сумма углов выпуклого пятиугольника равна -
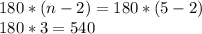
Если отношение углов ∠A : ∠В : ∠С : ∠D : ∠E = 4 : 4 : 2 : 3 : 2, то пусть каждый из них равен 4x, 4x, 2x ,3x, 2x соответственно.
4x+4x+2x+3x+2x = 540°
15x = 540°
x = 36°.
∠A = 4x = 4*36° = 144°
∠B = 4x = 4*36° = 144°
∠C = 2x = 2*36° = 72°
∠D = 3x = 3*36° = 108°
∠E = 2x = 2*36° = 72°.
ответ: 144°, 144°, 72°, 108°, 72°.
Дано:
ABCDE - выпуклый пятиугольник.
∠A : ∠В : ∠С : ∠D : ∠E = 4 : 4 : 2 : 3 : 2.
Найти:
∠A, ∠В, ∠С, ∠D, ∠E = ?
Сумма углов выпуклого n-угольника вычисляется по формуле -
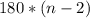
Где n - количество сторон.
Сумма углов выпуклого пятиугольника равна -
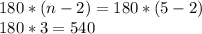
Если отношение углов ∠A : ∠В : ∠С : ∠D : ∠E = 4 : 4 : 2 : 3 : 2, то пусть каждый из них равен 4x, 4x, 2x ,3x, 2x соответственно.
4x+4x+2x+3x+2x = 540°
15x = 540°
x = 36°.
∠A = 4x = 4*36° = 144°
∠B = 4x = 4*36° = 144°
∠C = 2x = 2*36° = 72°
∠D = 3x = 3*36° = 108°
∠E = 2x = 2*36° = 72°.
ответ: 144°, 144°, 72°, 108°, 72°.

ответ: Ѕ=60 (ед. площади)
Объяснение:
Пусть дана трапеция АВСD. АС=15, ВD=8. КМ= средняя линия=8,5.
Из вершины С проведем параллельно BD прямую до пересечения с продолжением стороны АD в т.Е. Четырехугольник ВСЕD - параллелограмм (противоположные стороны параллельны). Поэтому DЕ=ВС, и АЕ=АD+ВС=2•КМ (т.к. средняя линия трапеции равна полусумме оснований).
S∆ АСЕ=h•АЕ:2. Площадь трапеции равна h•(АD+BC):2==h•АЕ:2. => площадь треугольника равна площади трапеции, т.к. высота трапеции и треугольника АСЕ общая. Площадь ∆ АСЕ можно найти по ф. Герона. Но можно иначе.
В ∆ АСЕ стороны равны: АС=15, СЕ=ВС=8, АЕ=2•8,5=17. Отношение сторон 8:15:17 - из Пифагоровых троек => ∆ АСЕ - прямоугольный. =>
S (АВСD)=S(АСЕ)=АС•СЕ:2=15•8:2=60 (ед. площади)