Відповідь:
Отримали від'ємне значення для BC², що неможливо в контексті задачі. Отже, така трапеція не існує з заданими сторонами.
Висновок: За заданими даними не можна знайти кути рівнобічної трапеції, оскільки така трапеція не існує.
Пояснення:
Для розв'язання цієї задачі використовуємо властивості рівнобічної трапеції.
Розглянемо рівнобічну трапецію з бічними сторонами AB і CD, діагоналями AC і BD, та кутом α між однією з бічних сторін і однією з діагоналей.
Дано:
AB = CD = 3 дм (дано бічна сторона)
AC = BD = 4 дм (дано діагональ)
Оскільки бічна сторона і діагональ перпендикулярні одна до одної, то ми можемо скласти прямокутний трикутник ABC, де AB - гіпотенуза, а AC - катет.
За теоремою Піфагора в прямокутному трикутнику ABC:
AB² = AC² + BC²
Для рівнобічної трапеції, AB = CD = 3 дм і AC = BD = 4 дм, отже:
3² = 4² + BC²
9 = 16 + BC²
BC² = 9 - 16
BC² = -7
в) AC >BC.
Объяснение:
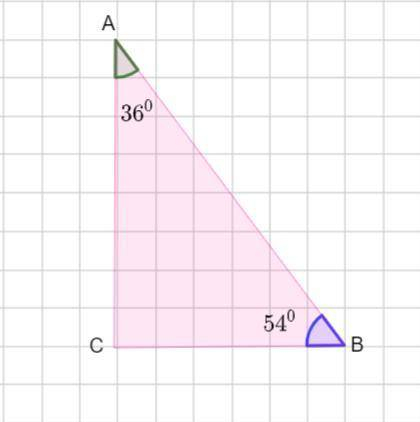
В треугольнике АВС известно, что ∠А = 36°, ∠В = 54°. Указать верное неравенство.
А) ВС > AB ; б) BC > AC; в) AC >BC; г) AC >AB.
Рассмотрим Δ АВС , ∠А = 36°, ∠В = 54°.
Так как сумма углов треугольника равна 180 °, то найдем третий угол ∠С .
∠С =180° - ( 36° +54°) = 180° -90° = 90°.
Тогда ΔАВС - прямоугольный с гипотенузой АВ . Гипотенуза всегда больше катетов. Поэтому утверждения А) ВС > AB и г) AC >AB неверны , так как в них катет больше гипотенузы.
В треугольнике напротив большего угла лежит большая сторона .
∠В > ∠ A, так как 54°> 36°. Тогда катет, лежащий напротив ∠В больше катета лежащего напротив ∠А. Тогда АС > BC и тогда верно утверждение в) AC >BC.
#SPJ1
гіпотенуза - (36:(3+4+5))*5=3*5=15