Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

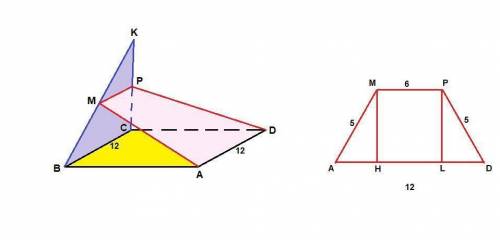
1) MPDA - равнобедренная трапеция
2) 36 см²
Объяснение:
1) МР - средняя линия треугольника ВСК, поэтому
МР║ВС и МР = 1/2 ВС = 6 см
МР║ВС, ВС║AD, ⇒ МР║AD.
Значит, MPDA трапеция. А так как МА = PD = 5 см, то
MPDA - равнобедренная трапеция.
2) Проведем высоты трапеции МН и PL. MPLH - прямоугольник, так как у него все углы прямые, тогда
HL = MP = 6 см.
ΔАМН = ΔDPL по гипотенузе и катету (∠АНМ = ∠DLP = 90°, так как проведены высоты, АМ = DP по условию и МН = PL как высоты), значит
АН = DL = (AD - HL)/2 = (12 - 6)/2 = 3 см
ΔАМН: прямоугольный, египетский, значит МН = 4 см.
Smpda = (MP + AD)/2 · MH = (6 + 12)/2 · 4 = 36 см²
Найдём проекцию ребра на плоскость основания пирамиды. Она равна половине диагонали квадрата, лежащего в основании. ПрРеб = 5 * cos 45 = 5/sqrt(2)
Заодно найдём проекцию апофемы (пригодится дальше), она равна половине стороны квадрата: ПрАп = 5/2 = 2,5.
Теперь найдём ребро L по теореме Пифагора: его квадрат равен сумме квадратов высоты пирамиды и проекции ребра: L = sqrt ( 7^2 + (5/sqrt(2))^2) = sqrt ( 49 + 12.5) = sqrt ( 49 + 12.5) = sqrt ( 61.5) = 7.842
Угол а между ребром и плоскостью основания измеряется линейным углом между ребром и проекцией ребра на плоскость основания: соs a = ПрРеб/L = (5/sqrt(2))/sqrt ( 61.5) = 3,536/ 7.842 = 0,4508. соs a = 63гр.
Апофема А пирамиды (высота треугольника, представляющего собой боковую грань, опущенная из вершины на сторону основания) равна: А = sqrt ( 7^2 + 2,5^2) = sqrt ( 49 + 6,25) = sqrt ( 55,25) = 7,433
Угол в между плоскостью грани и плоскостью основания измеряется линейным углом между апофемой и проекцией апофемы на плоскость основания: соs в = ПрАп/А = 2,5/sqrt ( 55,25) = 2,5/ 7,433 = 0,3363. соs в = 70гр.
Площадь поверхности пирамиды складывается из площади 4-х граней и основания: Sосн = a^2 = 5^2 = 25. Sгр = 0,5 А * a = 0.5 * 7,433 * 5 = 18,5825
S пир = Sосн + 4Sгр = 25 + 4 * 18,5825 = 25 + 74,33 = 99,33 кв.см
ответ:S пир = 99,33 кв.см. Угол наклона ребра к плоскости основания примерно равен 63гр., а угол наклона боковой грани к плоскости основания равен примерно 70гр.