Параллелограмм - это четырехугольник, у которого противолежащие стороны попарно параллельны.
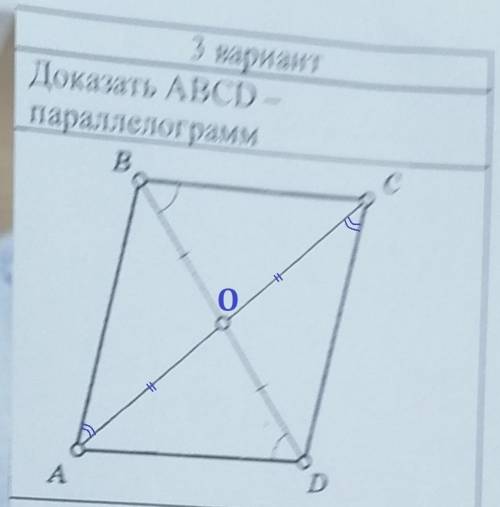
Если мы докажем, что BC║AD и AB║CD, то докажем, что ABCD параллелограмм.
1) ∠DBC = ∠BDA по условию, а это внутренние накрест лежащие углы при прямых BC и AD и секущей BD ⇒ BC║AD. (если внутренние накрест лежащие угли при двух прямых и секущей равны, то эти прямые параллельны).
2) ΔBOC = ΔAOD по второму признаку (стороне и двум углам):
BO = OD по условию, ∠OBC = ∠ODA по условию, ∠BOC = ∠AOD вертикальные углы.
В равных треугольниках соответствующие стороны равны. AO = OC
3) ΔAOB = ΔCOD по первому признаку:
BO = OD по условию, AO = OC по доказанному, ∠AOB = ∠COD - вертикальные углы.
Из равенства треугольников следует равенство соответствующих углов.
∠BAO = ∠DCO, это внутренние накрест лежащие углы при прямых AB и CD и секущей AC. ⇒ AB ║CD
4) В четырехугольнике ABCD AD║BC и AB ║ CD. Четырехугольник ABCD параллелограмм.
Доказано.
ВК=12 м
СВ=19,5 м
ОК=1,5 м
АК=х м
Найти: АК=? м
Решение
ΔАВС и ΔАКО подобны (подобие по двум углам).
Из отношения сторон подобных треугольников следует:
19,5:1,5=(12+х)/х
Выразим и найдем х:
19,5/1,5=(12+х)/х
19,5х=1,5(12+х)
19,5х=18+1,5х
19,5х-1,5х=18
18х=18
х=18:18
х=АК=1 метр
ОТВЕТ: длина тени человека 1 метр