*объяснения понять чуть проще, если сделать рисунки к каждой из задач*
1. ответ: 60°.
∠BAC=∠BCA=80° (как углы при основании равнобедренного треугольника)
∠DAC=1/2∠BAC=80°/2=40° (т. к. АD - биссектриса)
∠ADC=180°-(∠DCA+∠DAC)=180°-(80°+40°)=180°-120°=60° (сумма углов треугольника равна 180°)
2. ответ: 28°.
Т. к. сумма углов треугольника равна 180°, то третий угол равен 180°-71°-81°=28°.
3. ответ: 9°.
Сумма углов треугольника равна 180°, углы при основании равнобедренного треугольника равны. Значит, ∠С = (180°-162°)/2 = 18°/2 = 9°.
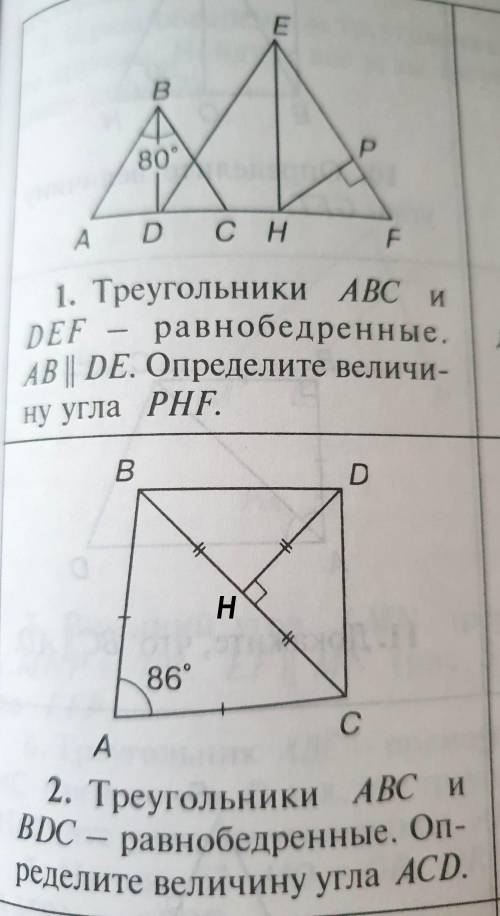
Задача: Треугольник ABC и DEF — равнобедренные. AB || DE, ∠ABC = 80°. Определить величину угла PHF.
Т.к. ΔABC равнобедренный (AB = BC), имея угол ABC, равный 80°, определим углы при основе AC:
∠BAC = ∠BCA = (180−80)/2 = 100/2 = 50°
∠BAC = ∠EDF = 50° — как соответственные при параллельных прямых AB и DE и секущей AF.
Т.к. ΔDEF равнобедренный (DE = EF), ∠EDF = ∠EFD = 50°.
Р-м ΔHFP:
∠FPH = 90°, PFH = 50° ⇒
⇒ ∠PHF = 180−∠FPH−∠PFH = 180−90−50 = 40°
ответ: Величина угла PHF равна 40°.
Задача: Треугольник ABC и BDC — равнобедренные. ∠BAC = 86°. Определить величину угла ACD.
Т.к. ΔABC равнобедренный (AB = AC), имея угол BAC, равный 86°, определим углы при основе BC:
∠ABC = ∠ACB = (180−86)/2 = 94/2 = 47°
Р-м ΔBDC:
Обозначим отрезок, соединяющий вершину D и сторону BC через DH.
BC = 1/2DH ⇒ DH — медиана
Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным, а медина проведена из прямого угла к гипотенузе ⇒
⇒ ΔBDC — прямоугольный, ∠BDC = 90°.
Т.к. ΔBDC равнобедренный (BD = CD), имея угол BDC, равный 90°, определим углы при основе BC:
∠DBC = ∠DCB = (180−90)/2 = 90/2 = 45°
Итого, ∠ACD будет равен:
∠ACD = ∠ACB+∠BCD = 47+45 = 92°
ответ: Величина угла ACD равна 92°.
Радиус описанной окружности равен половине диагонали
Диагональ равна 8√2 - по теореме Пифагора
Радиус описанной окружности = 4√2
ответ: 4√2 см