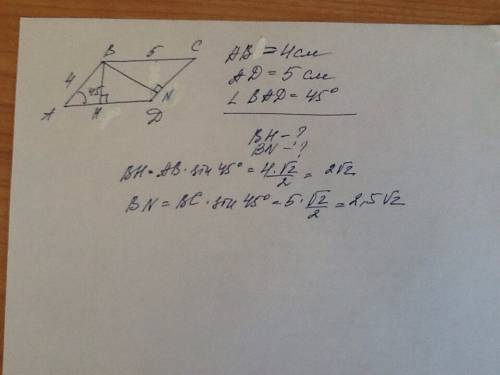
меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
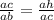
теперь подставим наши значения в эту пропорцию:
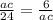
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

x=54° <A ,наибольший острый угол.
Объяснение:
<A+<B=90°
<A-<B=18°
<A=x
<B=90°-x
<B=x-18°
90°-x=x-18°
2x=90°+18°
2x=108°
x=108°:2
x=54° <A ,наибольший острый угол.
Если от 90°- <A =90°-54°=36° ,то видим,что при этом выполняется второе условие задачи: <С-<А=36°.Значит первый вариант решения нам подходит.
2
<A-<B=36°
<B=<A-36°
<B=90°-<A
<A=x
x-36°=90°-x
2x=90°+36°
2x=126°
x=126°:2
x=63° <A ,наибольший острый угол.
Если от 90°- <A =90°-63°=17° ,то видим,что при этом не выполняется второе условие задачи: <С-<А=18°.Значит второй вариант решения нам не подходит.