См. Объяснение
Объяснение:
Треугольник АВС равен треугольнику МКС, так как:
1) сторона ВС треугольника АВС равна стороне СК треугольника МКС - согласно условию;
2) угол ВСА треугольника АВС, прилежащий к стороне ВС, равен углу МСК, прилежащему как стороне СК треугольника МКС , - как углы вертикальные;
3) угол В, прилежащий к стороне ВС треугольника АВС, равен углу К прилежащему как стороне СК треугольника МКС - согласно условию.
Если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Следовательно, ΔАВС = ΔМКС, - что и требовалось доказать.
Объяснение:
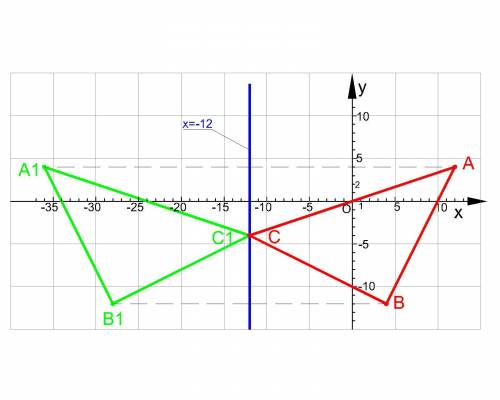
1. Выполняем построение треугольника АВС.
2. Строим график прямой х = -12 . Это вертикальная прямая проходящая через точку (-12; 0)
3. Выполняем построение симметричной фигуры:
от т. А проводим перпендикуляр к прямой х = -12. Откладываем перпендикуляр такой же длины в противоположною сторону от х = -12.
То же самое выполняем для т. В. Т. С совпадает с точкой С1, т.к. абсцисса т. С = -12 и лежит на прямой х = -12.
Координаты ΔA1B1C1 можно определить графически:
А1(-36;4) , В1(-28; -12) , С1(-12; -4).
Также абсциссы можем определить математически:
х1 = -12 - (12+х) = -24-х.
Здесь -12 - это сдвиг координат влево на 12 единиц, (12+х) расстояние между осью симметрии и точками исходного треугольника.
Ординаты остаются неизменными, т.к. ось симметрии - вертикальная.
Доказательство. Рассмотрим треугольник ABC с высотами AA1, BB1 и CC1 и докажем, что прямые AA1, BB1 и CC1 пересекаются в одной точке.
Проведем через точки A, B, C прямые, соответственно перпендикулярные к прямым AA1, BB1, CC1 и, следовательно, соответственно параллельные прямым BC, CA, AB (рис. 79). Эти прямые, пересекаясь, образуют треугольник A2B2C2.
Так как C2A || BC и C2B || AC, то четырехугольник BC2AC — параллелограмм, поэтому C2A = BC. По аналогичной причине AB2 = BC. Из этих двух равенств следует, что C2A = AB2, т. е. точка A — середина отрезка C2B2. Аналогично можно доказать, что точки B и C — середины отрезков A2C2 и A2B2.
Таким образом, прямые AA1, BB1, CC1 являются серединными перпендикулярами к сторонам треугольника A2B2C2, поэтому они пересекаются в одной точке. Теорема доказана.
Точку пересечения высот треугольника (или их продолжений) для краткости называют ортоцентром треугольника.
Итак, с каждым треугольником связаны четыре точки: точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам, точка пересечения медиан и ортоцентр. Эти четыре точки называются замечательными точками треугольника.