Из середины O отрезка AB проведем перпендикуляр OH к прямой a (См рис (в).). На прямой b от точки B отложим отрезок BH1, равный отрезку AH и проведем отрезок OH1. Треугольники OHA и OH1B равны по двум сторонам и углу между ними (AO=BO, AH=BH1, угол 1= угол 2), по этому угол 3 = угол 4 и угол 5 = угол 6. Из равенства угол 3 = угол 4 следует, что точка H1, лежит на продолжении луча ОН, т.е. точки Н, О и Н1 лежат на одной прямой, а из равенства угол 5 = угол 6 следует, что угол 6 - прямой. Итак прямые a и b парпендикулярны к прямой YY1, поэтому они параллельны. Теорема доказана.

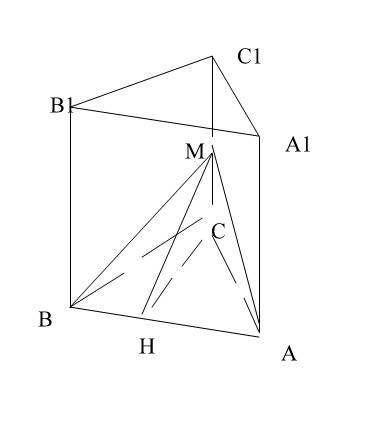
Дана прямая треугольная призма АВСА1В1С1.
Угол МНС=60 гр. НС-высота треугольника АВС.
Рассмотрим треугольник АВС и ВНС.
Эти треугольники подобны, следовательно, ВН/ВС = СН/АС = ВС/АВ.
Берем первое и последнее соотношение пропорции и получаем, что ВН = ВС^2 / АВ.
Треугольник ВНС-прямоугольный, следовательно, BC^2 = BH^2 + CH^2.
СН = (ВС *АС) / АВ
СН = (6*8)/10=4,8.
Рассмотрим треугольник НСС1-прямоугольный. Угол МНС=60 гр, следовательно угол СС1Н=30 гр. Катет, лежащий, напротив угла 30 градусов, равен половине гипотенузы.
СН = 1/2 МН
МН = 2*4,8=9,6.
Вроде так.
8=1/3*12*h
8=4h
h=2 - высота пирамиды
2) V=1/3S(осн)h
16=1/3S(осн)4
16=4/3S(осн)
S(осн)=12 - площадь основания пирамиды