1. 4 см.
2. 84 см.
3. 2√26 см.
Объяснение:
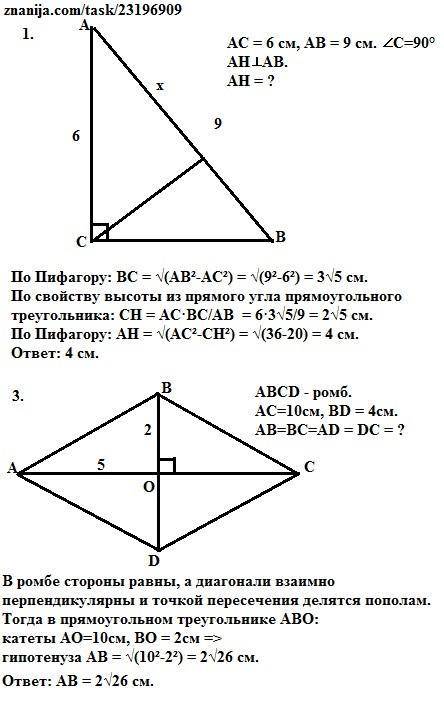
1. По Пифагору: ВС = √(АВ²-АС²) = √(9²-6²) = 3√5 см.
По свойству высоты из прямого угла прямоугольного треугольника:
СН = АС·ВС/АВ = 6·3√5/9 = 2√5 см.
По Пифагору: АН = √(АС²-СН²) = √(36-20) = 4 см.
ответ: 4 см.
2. По Пифагору второй катет равен √(37²-35²) = √(2·72) = 12см. Тогда периметр треугольника (сумма его трех сторон) равен:
37+35+12 = 84см.
ответ: 84см.
3. В ромбе стороны равны, а диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.
Тогда в прямоугольном треугольнике АВО:
катеты АО=10см, ВО = 2см =>
гипотенуза АВ = √(10²-2²) = 2√26 см.
ответ: 2√26 см.
AE - биссектриса A => BAE=EAD=a - обозначим
углы BKA=EKD как вертикальные
AKD+DKE = 180 как смежные
по т.синусов из треуг.BAK можно записать:
BK:sina = AB:sin(BKA)
по т.синусов из треуг.KAD можно записать:
KD:sina = AD:sinAKD = AD:sin(180-EKD) = AD:sin(EKD) = AD:sin(BKA)
т.к. sin(180-a) = sina в треугольнике
отсюда sin(BKA) = AD * sina / KD
BK:sina = AB:sin(BKA) => BK:sina = AB: (AD * sina / KD) = AB * KD / (AD * sina) =>
BK = AB * KD / AD
BK / KD = AB / AD = AB / BC (т.к. параллелограмм) = 4/9
2)4+1=5(частей)-приходится на отрезок АВ.
3)7,5:5=1,5(см)-длина отрезка СВ.