Даны четыре точки - три из них всегда лежат в одной плоскости. Пусть это будут точки А, В и С. Тогда четвертая точка - D - не лежит в этой плоскости.
Рисунок к задаче в приложении. Получили пирамиду. У неё четыре вершины. В каждой вершине пересекаются 3 пары рёбер. Всего пересекающихся пар прямых будет: N = 4*3 = 12 .
Запишем такие пары прямых:
ABxAC, ABxAD, ACxAD - три из вершины А.
BAxBD, BAxBC, BCxDD - три из вершины В.
CAxCB, CBxCD, CAxCD - три из вершины С.
DAxDB, DBxDC, DCxDA - три из вершины D.
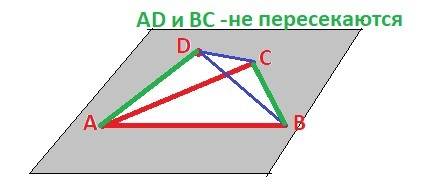
А вот прямые AD и BC - не пересекаются.
Тр-ник, образованный сторонами парал-ма и диагональю, прямоуг-ный, след-но
5*sinA=3; => sinA=3/5=0.6, Sосн=5*4*3/5=12
апофема1=sqrt(4+4)=2sqrt2; апофема 2=sqrt(4+6.25)=sqrt10.25; Sб1=2*2sqrt2=4*sqrt2;
Sб2=(1/2)*5*sqrt10.25; => Sполн=Sосн+2Sб1+2Sб2