1. Расстояние от центра окружности до точки, из которой проведены две касательные, делит угол A пополам. Значит угол HAO равен 30 градусам. Проведем радиус от точки O в точку касания окружности с касательной. Радиус, проведенный из центра окружности к точке касания является перпендикуляром к касательной. Получается прямоугольный треугольник HAO. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов половине гипотенузы. OA - гипотенуза
OH=1/2*6
OH=3
OH-радиус окружности
ответ:R=3
2.28 градусов
3.7
Перша сторона АС=16см
Друга сторона АВ=20см
Третя сторона ВС=24см
Объяснение:
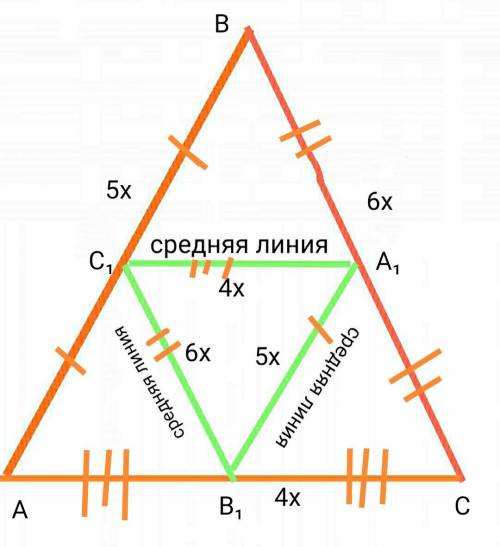
Позначемо вершини трикутника АВС, а вершини трикутника створеного середніми лініями А₁В₁С₁. Вершини ∆А₁В₁С₁ лежать на серединах сторін ∆АВС, тому вони ділять сторони ∆АВС навпіл. А також середня лінія трикутника паралельна протилежній стороні і дорівнює її половині, тому: АС₁=ВС₁=А₁В₁; АВ₁=СВ₁=А₁С₁; ВА₁=А₁С=В₁С₁, тому ∆А₁В₁С₁~∆АВС. Якщо середні лінії ∆А₁В₁С₁ відносяться як 4 : 5 : 6, то сторони ∆АВС будуть мати таке ж саме відношення. Позначемо ці відношення як 4х, 5х та 6х, і якщо відомо, що периметр трикутника 60см, складемо рівняння:
4х+5х+6х=60
15х=60
х=60÷15
х=4
Тоді перша сторона АС=4×4=16см
Друга сторона АВ=5×4=20см
Третя сторона ВС=6×4=24см
мне просто нужны !