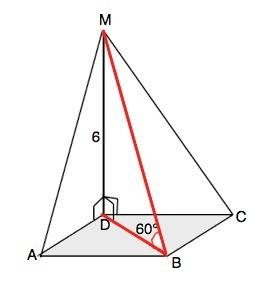
а) По условию MD перпендикулярна плоскости квадрата,
АD -проекция АМ на плоскость квадрата.
СD - проекция СМ на плоскость квадрата.
По т. о 3-х перпендикулярах МА⊥АВ, и МС⊥СВ.
Углы МАВ и МСВ прямые,⇒ ∆ МАВ и Δ МСВ прямоугольные.
б) В прямоугольном ∆ МDB катет DB равен MD:tg60°=6:√3=2√3
BD- гипотенуза прямоугольного равнобедренного ∆ ABD, его острые углы=45°.
АВ=ВD•sin45°=2√3•√2/2=√6
в) МD перпендикулярна плоскости квадрата по условию.
В ∆ АВD катет АD является проекцией наклонной АМ на плоскость квадрата.
Гипотенуза DB является проекцией МВ на плоскость квадрата.
АВ - общий катет ∆ АМВ и ΔΔ ADB. ⇒ ∆ ABD является проекцией ∆ MAB на плоскость квадрата.
в) В ∆ МАВ по т. о 3-х перпендикулярах наклонная МА⊥АВ,⇒
∆ МАВ прямоугольный.
Ѕ=AM•AB:2
Из ∆ АМD по т.Пифагора АМ=√(MD²²+AD²²)=√(36+6)=√42
S=√42•√6=√(7•6•6)=6√7 см²
Зная: sin2α = 2sinαcosα
cos3α = cos3α – 3cosα
sin(2∙18°)=cos(3∙18°); 2sin18°∙cos18°=4cos³18°-3cos18°
Заметим, что можно сократить cos18°
2sin18°=4cos²18°-3
Зная, что cos²18°=1-sin18°
4sin ²18°+2sin18°-1=0