Каждое ребро правильной шестиугольной призмы равно а. Найдите площадь поверхности призмы.
---
Призма называется правильной, если ее боковые ребра перпендикулярны основаниям, а основания – правильные многоугольники.
Все ребра правильной призмы равны, ⇒
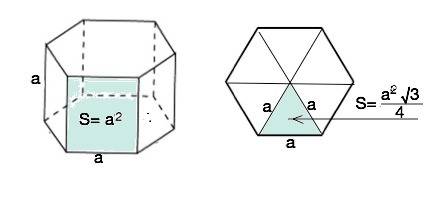
каждая из 6 боковых граней – квадрат, площадь которого S=a².
Ѕ(бок)=6а²
Основания правильной шестиугольной призмы - правильные шестиугольники, состоящие из 6 равных правильных треугольников.
Формула площади правильного треугольника S=(a²√3):4 ⇒
Ѕ (осн)•2=2•6•(a²√3):4=3а²√3
Площадь поверхности призмы равна сумме площадей: площади боковой поверхности и двух оснований.
S (призмы)= 6а²*+3•a²√3 или 3а²•(2+√3) ≈11,2а²
Объяснение:
Все грани прямоугольного параллелепипеда - прямоугольники.
ΔА₁АС: ∠A₁AC = 90°
sinβ = AA₁ / A₁C, ⇒ AA₁ = A₁C · sinβ,
AA₁ = a · sinβ
cosβ = AC / A₁C, ⇒ AC = A₁C · cosβ,
AC = a · cosβ.
Точка пересечения диагоналей прямоугольника является центром описанной окружности. Тогда для окружности, описанной около прямоугольника ABCD ∠АОВ - центральный, а ∠ACB - вписанный, опирающийся на ту же дугу, значит
∠АCB = 1/2 ∠AOB = α/2.
ΔABC: ∠ABC = 90°
sin∠ACB = AB / AC, ⇒ AB = AC · sin∠ACB,
AB = a · cosβ · sin(α/2),
cos∠ACB = BC / AC, ⇒ BC = AC · cos∠ACB,
BC = a · cosβ · cos(α/2).
Sбок = Pосн · AA₁
Sбок = (AB + BC) · 2 · AA₁
Sбок = (a · cosβ · sin(α/2) + a · cosβ · cos(α/2)) · 2 · a · sinβ =
= a · cosβ(sin(α/2) + cos(α/2)) · 2 · a · sinβ =
= 2a²sinβ·cosβ(sin(α/2) + cos(α/2)) =
= a²sin2β (sin(α/2) + cos(α/2))