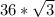Скрещивающиеся прямые, это прямые, которые не лежат в одной плоскости.
а) Предположим, это не так. Тогда МА и ВС лежат в одной плоскости. Знасит МА и ВС пересекабтся или параллельны. Если они пересекаются, то прямая МА имеет ещё одну общую точку с плоскостью АВСD и значит, лежит в этой плоскости. Противоречие. Если же АМ параллельна ВС, То АМ и ВС образуют плоскость АМВС. Эта плоскости пересекает плоскость АВСD по прямой ВС и имеет с ней общую точку М. Значит эти плоскости совпадают. Значит МА лежит в плоскости АВСD. Противоречие. Наше предположение неверно, МА и ВС - скрещивающиеся прямые.
б)Угол МАD - угол между векторами АМ и АD. Но вектор СВ равен вектору АD, поэтому угол между АМ и СВ равен 45 градусов
правильная пирамида - все углы равны и стороны равны.Таким образом, задан тетраэдр.
плоский угол при вершине - угол между двумя ребрами.
Пусть боковая сторона равна а.
Рассмотрим прямоугольный треугольник ABC, образованный боковой стороной тетраэдра, её проекцией на основание и высотой пирамиды.
Ясно, что основание высоты равноудалено от вершин основания, то есть проекция бокового ребра на основание есть радиус R описанной окружности вокруг треугольника со стороной а, т. е. R =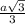
;
Заданный отрезок длины 3 является в построенном прямоугольном треугольнике МЕДИАНОЙ, то есть равен половине гипотенузы. А роль гипотенузы играет боковое ребро. Поэтому а = 6
Площадь правильного треугольника со стороной 6 равна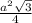 
= 
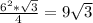6^2*√3/4; а всего у нас 4 одинаковых грани, то есть площадь всей поверхности пирамиды равна
