
ВОТ
Объяснение:
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 2 : 3, считая от вершины угла при основании треугольника. Найдите основание треугольника, если его боковая сторона равна 15 см
Объяснение:
ΔАВС, АВ=ВС=15 см, К, Р, М-точки касания окружности сторон АВ,ВС,АС соответственно,АК/КВ=2/3. Найти АС.
Отрезок АВ , по условию , состоит из 5 частей или 15 см⇒
1 часть равна 3 см. Тогда АК=6см .
Т.к. АВ=ВС, то СР/РВ=2/3.
По свойству отрезков касательных , проведенных из одной точки :
АК=АМ=6 см, МС=СР=6 см ⇒ АС=АМ+МС=6+6=12(см
Подробнее - на -
1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
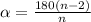
Найдем при каком n угол будет равен 160°:
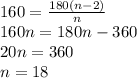
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
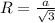
Подставим заданное значение стороны:
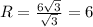
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
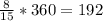 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см