Периметр паралелограма 60 см, а одна из сторон 10см. найдите вторую сторону паралелограма

Question

Геометрия: Периметр паралелограма 60 см, а одна из сторон 10см. найдите вторую сторону паралелограма

elleonoel · Accepted Answer

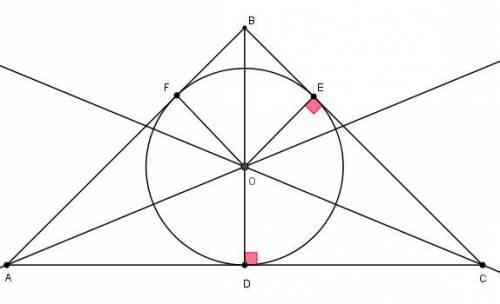
Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности и всегда находится внутри треугольника. Пусть OD = 3x и OB = 5x. CD = CE как касательные к окружности; OE = OD = 3x как радиусы, проведенные в точку касания.

По условию 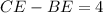CE-BE=4 . По т. Пифагора из треугольника BOE

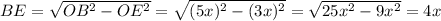
$BE=\sqrt{OB^2-OE^2}=\sqrt{(5x)^2-(3x)^2}=\sqrt{25x^2-9x^2}=4x$

Далее из прямоугольного треугольника BDC по т. Пифагора:

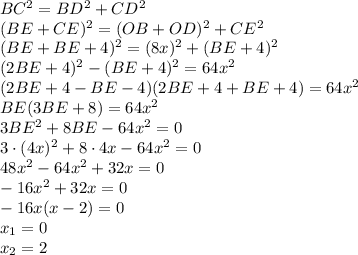
$BC^2=BD^2+CD^2\\ (BE+CE)^2=(OB+OD)^2+CE^2\\ (BE+BE+4)^2=(8x)^2+(BE+4)^2\\ (2BE+4)^2-(BE+4)^2=64x^2\\ (2BE+4-BE-4)(2BE+4+BE+4)=64x^2\\ BE(3BE+8)=64x^2\\ 3BE^2+8BE-64x^2=0\\ 3\cdot (4x)^2+8\cdot 4x-64x^2=0\\ 48x^2-64x^2+32x=0\\ -16x^2+32x=0\\ -16x(x-2)=0\\ x_1=0\\ x_2=2$

Первый корень не удовлетворяет условию, значит x = 2 см.

Тогда BE = 4x = 8 см, значит CE = BE + 4 = 8 + 4 = 12 см

CD = CE = 12 см, а так как BD является медианой и высотой, то

AC = 2 * CD = 2 * 12 = 24 см; AB = BC = CE + BE = 12 + 8 = 20 см

P = AB + BC + AC = 20 + 20 + 24 = 64 см.

Зточки перетину бісектрис рівнобедреного трикутника опущено перпендикулярно до бічної сторони, що ді

MOGZ ответил