Площадь треугольника находится как половина произведения стороны и высоты к ней проведенной, поэтому:
1) находим длину высоты из условия задачи 5х2=10 см
2) находим поладь 1/2*5*10=25 см2
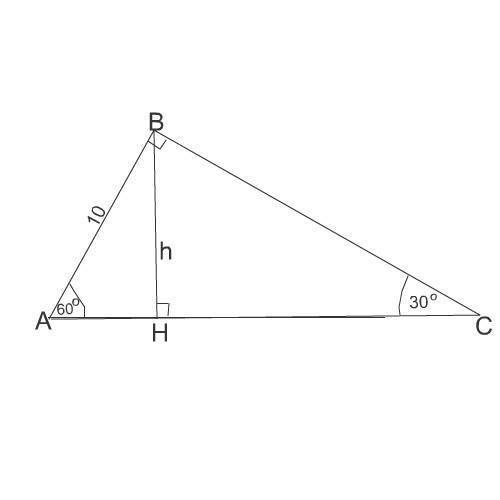
Задачу можно решить по-разному Обозначим вершины треугольника А, В, С, а точку пересечения высоты с гипотенузой - Н.
Найдем гипотенузу.
Так как катет АВ, равный 10 см, противолежит углу 30 градусов, он равен половине гипотенузы, а гипотенуза, соответственно, в два раза больше катета.
Гипотенуза равна 20 см
Катет ВС найдем по теореме Пифагора. Он равен 10√3
Пусть отрезок АН будет х, тогда НС - 20-х
Выразим h² из прямоугольных треугольников АВН и ВСН, образованных катетами, высотой и частью гипотенузы.
h²=АВ²-АН²= 10²-х²
h²=ВС²-НС²=(10√3)²-(20-х)²
Приравняем выражения, найденные для высоты.
10²-х²=(10√3)²-(20-х)²
100-х²=300-400+40х-х²
40х=200
х=5
Подставим значение х в уравнение высоты:
h²=АВ²-х гораздо короче, если мы помним значение синусов некоторых углов.
Рассмотрим треугольник АВС.
Высота, проведенная к гипотенузе, - катет прямоугольного треугольника АВН.
ВН:АВ=sin(60º)
sin(60º)=(√3):2
ВН=АВ*(√3):2=10*(√3):2=5√3
h=5√3
ромб - параллелограмм, у кот.все стороны равны
диагонали ромба перпендикулярны и делятся точкой пересечения пополам (как и у любого параллелограмма)
диагонали ромба - биссектрисы его углов
ромб ABCD AB=BC... AB=BD => треугольник ABD - равносторонний
в равностороннем треугольнике все стороны и все углы равны => BAD = 180/3=60 = BDA = DBA
BD - биссектриса CDA => CDA = 2BDA = 2*60 = 120
BAD = BCD, CDA = CBA (т.к. ромб - это параллелограмм)
вторая диагональ AC = AO + OC
из ABO (AB=10, BO=5) по т.Пифагора AO = корень(10*10-5*5) = корень(100-25) = корень(75) = корень(25*3) = 5*корень(3)
дано сторона А=5см, тогда высота 5*2=10 S=/а*h/:2 S=/5*10/:2 S=25