Прямые ab и cd не являются параллельными.
Объяснение:
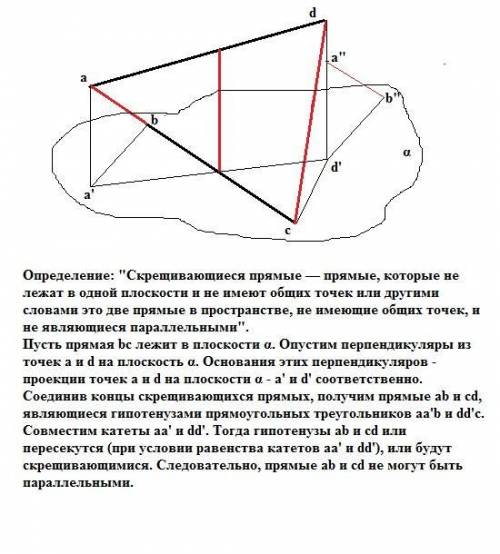
Определение: "Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными".
Пусть прямая bc лежит в плоскости α. Опустим перпендикуляры из точек a и d на плоскость α. Основания этих перпендикуляров - проекции точек а и d на плоскости α - a' и d' соответственно. Соединив концы скрещивающихся прямых, получим прямые ab и cd, являющиеся гипотенузами прямоугольных треугольников aa'b и dd'c. Совместим катеты aa' и dd'. Тогда гипотенузы ab и cd или пересекутся (при условии равенства катетов aa' и dd'), или будут скрещивающимися. Следовательно, прямые ab и cd не могут быть параллельными.

тогда сумма двух других острых углов тоже равна 90°
отношение 2:7 говорит, что 90 ° поделено на 7+2 =9 частей
90:(2+7) = 90:9 = 10° - 1 часть, тогда меньший угол
10*2 = 20°