Объяснение:
1. На любой прямой можно взять сколько угодно точек, принадлежащих этой прямой и не принадлежащих этой прямой.
Другая прямая, хоть параллельная, хоть перпендикулярная, ни при чём.
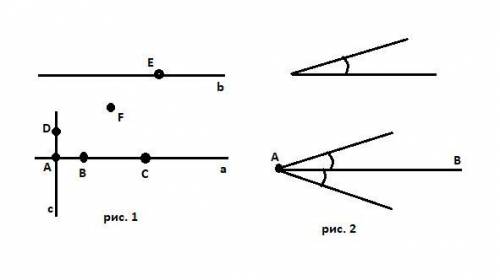
Смотрите рис. 1.
Точки A, B, C принадлежат прямой а.
Точки D, E, F не принадлежат прямой а.
Точка Е принадлежит параллельной прямой b.
Точка D принадлежит перпендикулярной прямой c.
Точка А принадлежит и прямой а и прямой с.
2. Два угла можно построить на одном луче, с двух разных сторон.
Смотрите рисунок 2.
Угол образец сверху. Снизу два угла, равных образцу, у луча AB.
Задание. Найдите радиусы вписанной и описанной окружностей правильного треугольника,если их разность равна 11 см.
r= \dfrac{a}{2 \sqrt{3} }r=
2
3
a
- радиус вписанной окружности;
R=\dfrac{a}{\sqrt{3} }R=
3
a
- радиус описанной окружности;
Их разность R-r=\dfrac{a}{\sqrt{3} } -\dfrac{a}{2\sqrt{3} } = \dfrac{2a}{2\sqrt{3} } -\dfrac{a}{2\sqrt{3} } =\dfrac{a}{2\sqrt{3} }R−r=
3
a
−
2
3
a
=
2
3
2a
−
2
3
a
=
2
3
a
и равен 11, т.е. \dfrac{a}{2\sqrt{3} } =11
2
3
a
=11 откуда a=22 \sqrt{3}\,\, _{CM}a=22
3
CM
Радиус вписанной окружности равен : r= \dfrac{22 \sqrt{3} }{2 \sqrt{3} } =11\,\,\, _{CM}r=
2
3
22
3
=11
CM
а радиус описанной окружности: R= \dfrac{a}{ \sqrt{3} } = \dfrac{22 \sqrt{3} }{ \sqrt{3} } =22\,\, _{CM}R=
3
a
=
3
22
3
=22
CM
ответ: 11 см и 22 см.
Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника, т.е. в данном треугольнике a/b=5/8
8a=5b
b=8a/5=1,6b
а+b=91
1,6b+b=91
2,6b=91
b=91:2,6
b=35
a=1,6b=1,6*35=56
ответ: стороны треугольника равны 56 см и 35 см.