41.76 cм
6°
6°
168°
Объяснение:
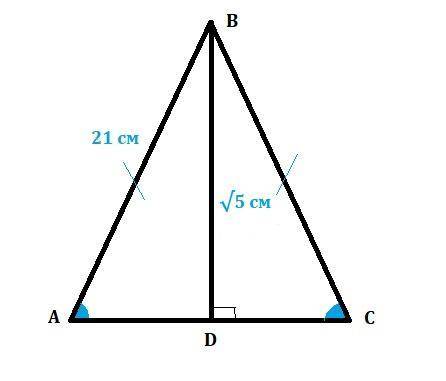
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.АВ=ВС=21см
Рассмотрим прямоугольный ΔAВD(∠D=90°)
По теореме Пифагора найдём катет AD:
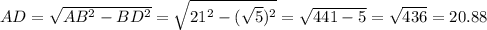
AC=2*AD=2*20.88=41.76 cм
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе: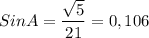
По таблице синусов находим значение угла А:
∠ А ≅ 6°
В равнобедренном треугольнике углы при основании равны.∠С = ∠ А ≅ 6°
Сумма углов треугольника равна 180°
∠В = 180-∠А-∠С = 180-6-6=168°
Из некоторой точки А (черт. 4) проведены к данной плоскости Р перпендикуляр АО = 1 см и две равные наклонные ВА и АС, которые образуют с перпендикуляром / ВАО = / СAO = 60°, а между собой / САВ = 90°. Найти расстояние ВС между основаниями наклонных.
2) Из данной точки проведены к данной плоскости две наклонные, равные каждая 2 см; угол между ними равен 60°, а угол между их проекциями — прямой. Найти расстояние данной точки от плоскости.
3) Из некоторой точки проведены к данной плоскости две равные наклонные; угол между ними равен 60°, угол между их проекциями — прямой. Найти угол между каждой наклонной и её проекцией.
высота в кв=100-9=91
S=h(a+b):2
S=корень из 91×(12+18):2= корень из 91×15