ответ: 20 см
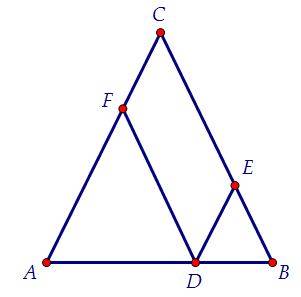
Решение: смотри рисунок.
Пусть треугольник BAC равнобедренный, AB=AC=10 см.
Возьмем произвольную точку K на основании BC и проведем KM||AC иKN||AB
KM=AN, KN=AM -противоположные стороны параллелограмма.
Докажем, что KM=BM. Угол 2=углу 4 как соответственные углы при AC||KM и секущей KC. Но угол 4=углу 1 (углы при основании равнобедренного треугольника). Отсюда угол 2=углу 1. Значит треугольник BMK равнобедренный и KM=BM как его боковые стороны.
Аналогично докажем, что KN=NC. Угол 3=углу 1 как соответственные углы при AB||KN и секущей KB. Но угол 1=углу 4 (углы при основании равнобедренного треугольника). Отсюда угол3 =углу 4. Значит треугольник KNC равнобедренный и KN=NC как его боковые стороны.
Периметр параллелограмма =KM+MA+AN+NK=BM+MA+AN+NC=BA+AC=10+10=20 (см)
Задание 8. В правильной четырёхугольной пирамиде SABCD точка О — центр основания, S — вершина, CS = 17, BD = 16. Найдите длину отрезка SO.
Решение.
В основании правильной четырехугольной пирамиды лежит квадрат, следовательно, диагонали BD=AC, а вершина O, лежащая на их пересечении, делит диагонали пополам. Рассмотрим прямоугольный треугольник SOC с гипотенузой SC=17 и катетом OC=16:2=8. По теореме Пифагора находим SO:
.
ответ: 15.