Объяснение:
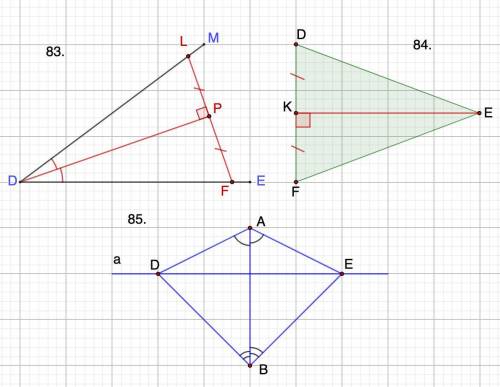
83.
Дано: ∠MDE;
DP ⊥ LF; PL = PF.
Доказать: ∠LDP = ∠FDP.
Доказательство:
Рассмотрим ΔDLP и ΔDPF - прямоугольные (DP ⊥ LF).
PL = PF (условие)
DP - общая.
⇒ ΔDLP = ΔDPF (по двум катетам)
В равных треугольниках против равных сторон лежат равные углы.⇒ ∠LDP = ∠FDP.
84.
Дано: ΔDEF;
EK ⊥ DF; DK = FK;
Доказать: ED = EF.
Доказательство:
Рассмотрим ΔKDE и ΔKEF - прямоугольные (EK ⊥ DF) .
DK = FK (условие)
КЕ - общая.
⇒ ΔKDE = ΔKEF (по двум катетам)
В равных треугольниках против равных углов лежат равные стороны.⇒ ED = EF.
85.
Дано: прямая а;
∠DAB = ∠EAB; ∠DBA = ABE;
Доказать: ΔBAD = ΔBAE.
Доказательство:
Рассмотрим ΔBAD и ΔBAE.
∠DAB = ∠EAB; ∠DBA = ABE (по условию)
АВ - общая.
⇒ ΔBAD и ΔBAE (по стороне и двум прилежащим углам. 2 признак)
Если мы представим себя в роли наблюдателя, стоящего в начале координат и обращенного в сторону положительной полуоси х, то в случае а) ось у будет идти справа налево, а в случае б) — слева направо; В первом случае координатную систему называют правой, во втором левой.
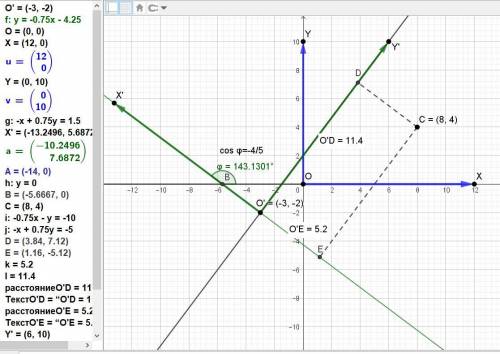
Координаты точки C в новой и старой системе координат связаны соотношениями с учётом того, что они имеют разную ориентацию – старая система правая, а новая - левая:
{x'=(x-a)* cosφ + (y-b)*sinφ
{y'=(y-a)*sinφ - (y-b)*cosφ.
Для заданных условий: a = -3, b = -2, cosφ=-4/5, sinφ=√(1-(-4/5)^2 )=3/5.
Проверим координаты точки С(8; 4) в новой (левой) системе.
x’ = (8-(-3))*(-4/5) + (4-(-2)*(3/5) = (-44/5) + (18/5) = -26/5 = -5,2.
y’ = (8-(-3))*(3/5) - (4-(-2)*(-4/5) = (33/5) - (-24/5) = 57/5 = 11,4.
На прилагаемом графике видно, что расчёт верен.
Правильный тетраэдр - треугольная пирамида, все грани которой правильные треугольники.
Обозначим пирамиду МАВС, центры eё граней E,P,T.
Основание О высоты МО пирамиды - центр описанной (и вписанной) окружности равностороннего ∆ АВС.
а) Выразить m через h.
АО - радиус описанной окружности.
Формула R=m/√3
MO²=АМ²-АО²
h²=m²-m²/3
2m²=3h
m=h√(3/2)=(h√6)/2
б) Выразить n через m.
Центр правильного треугольника - точка пересечения его медиан. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. В таком же отношении делятся ребра пирамиды.
МТ:ТН=2:1, Mc:MC=2:3; ⇒ cb:CB=2:3
Центры граней лежат в плоскости, параллельной основанию АВС и образующей в сечении треугольник abc~АВС с коэффициентом подобия k=2/3. ab=bc=ac-=2/3m
Расстояния между центрами граней - стороны треугольника, образованного при соединении центров граней, ∆ abc~ ∆ РТЕ с k=1/2.
n=ab/2=1/2•(2/3)m
n=m/3.