Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
V=⅓ S∙h
Основание правильного шестиугольника состоит из шести правильных треугольников.
Площадь правильного треугольника находят по формуле:
S=(а²√3):4
S=4√3):4=√3
Площадь правильного шестиугольника в основании пирамиды:
S=6√3
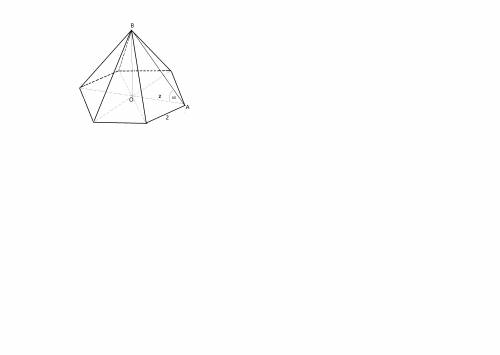
Высоту найдем из прямоугольного треугольника АВО:
Так как ребро образует с с диагональю основания угол 60°, высота пирамиды ВО равна
H=ВО=2:ctg (60°)= 2·1/√3=2√3
Можно найти высоту и по т. Пифагора с тем же результатом.
V= 2√3∙6 √3:3=12 (кубических единиц)
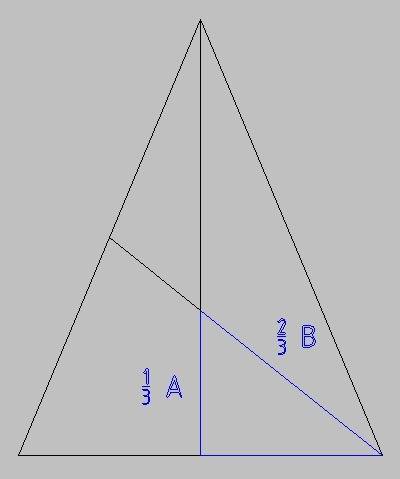
б)Тогда из свойств биссектрис треугольника следует, что AC/BC=AD/BD.
в) Но по требованию равноудалённости биссектрисы до точек A и B должно быть AD=BD, тогда и AC=BC, тогда, ответ: точка лежащая на биссектрисе угла C на одинаковом расстоянии от вершин A и B находится на средине стороны AB равнобедренного треугольника, у которого AC=BC.