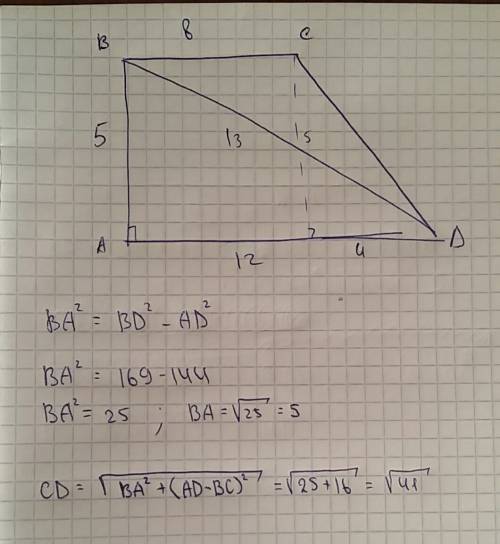
tg α =40/9.
sin α=40/41
cos α=9/41.
Объяснение (подробно):
Котангенсом угла (ctg α ) в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Тангенсом называется отношение противолежащего катета к прилежащему.
Если прилежащий катет равен 9, то противолежащий - 40.
Катеты 9 и 40 - из пифагоровых троек (Пифагоровыми тройками чисел называются числа, равные длинам сторон прямоугольного треугольника и удовлетворяющие формуле Пифагора. Причем, не существует пифагоровых троек, для которых гипотенуза и один из катетов являются катетами другой пифагоровой тройки). Поэтому для данного сочетания катетов гипотенуза равна 41 ( проверьте по т.Пифагора).
Итак, если ctg α=9/40, то тангенс - число, обратное данному, т.е. tg α =40/9.
Синус - отношение противолежащего катета к гипотенузе:
sin α=40/41,
соответственно косинус угла = отношение прилежащего катета к кипотенузе:
cos α=9/41.
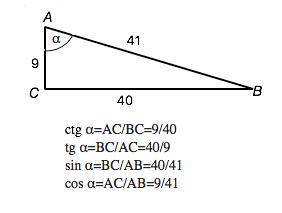
ответ: я точно не знаю, но если не правильно извините.
а)даны стороны треугольника ав и ас и угол между ними.
на произвольной прямой отложим отрезок, равный длине стороны ас, отметим на нём точки а и с.
из вершины а заданного угла проведем полуокружность произвольного радиуса и сделаем насечки м и к на его сторонах. ам=ак= радиусу проведенной окружности.
из т.а на отложенном отрезке тем же раствором циркуля проведем полуокружность. точку пересечения с ас обозначим к1.
от к1 циркулем проведем полуокружность радиусом, равным длине отрезка км, соединяющим стороны заданного угла.
эта полуокружность пересечется с первой. через точку пересечения проведем от т. а луч и отложим на нем отрезок, равный данной стороне ав, отметим точку в. соединим в и с.
искомый треугольник построен.
биссектриса проводится так же, как проводится срединный перпендикуляр к отрезку.
из точек, взятых на сторонах угла на равном расстоянии от его вершины а ( отмеряем циркулем) проводим полуокружности равного радиуса так, чтобы они пересеклись. через точки их пересечения и а проводим луч. треугольник ам1к! - равнобедренный по построению, ае - перпендикулярен м1к1 и делит его пополам.
треугольники аем1 и аек1 равны по гипотенузе и общему катету. поэтому их углы при а равны. ае - биссектриса.