Объяснение:
Очевидно, что внутри отрезка AB такой точки существовать не может (если бы существовало, тогда сумма двух меньших отрезков должна быть больше длины исходной, что является противоречием), поэтому эта точка должна лежать где-то за пределами отрезка (по условию же сказано, что нужно найти точки на прямой, а не внутри отрезка).
Пусть l - расстояние от искомой точки X до A, тогда l + 6 - это расстояние от X до B. Тогда справедливо уравнение:
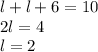
Значит, точка X должна отстоять от точки A на 2 см
Выглядит схематично это так:
2см 6см
---------------|----------------|------------------------------------------|----------------->
X A B
Это справедливо и для случая:
6см 2см
------------------|------------------------------------------|-------------|--------->
A B X
Больше таких точек нет.
Трапеция АВСД, АВ=СД, ВС=3,6, АД=10
проводим высоты ВН=СК на АД, треугольник АВН = треугольнику КСД по гипотенузе АВ=СД, и острому углу уголА=угол Д, АН=КД, четырехугольник НВСД прямоугольник, ВС=НК=3,6, АН=КД= (АД-НК)/2= (10-3,6)/2=3,2
оКРУЖНОСТЬ МОЖНО ВПИСАТЬ в трапецию когда сумма оснований = сумме боковых сторон, ВС+АД=АВ+СД, 3,6+10=АВ+СД, АВ=СД=13,6/2=6,8
треугольник АВН, ВН = корень (АВ в квадрате - АН в квадрате) =КОРЕНЬ (46,24-10,24)=6
ВН = диаметру окружности = 6, радиус=6/2=3
Площадь круга = пи х радиус в квадрате = 9пи