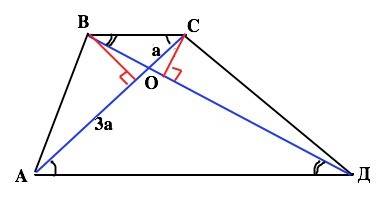
Диагонали трапеции «высекают» в ней подобные треугольники. ∆ВОС~∆ АОД по равным углам: углы при основаниях равны как накрестлежащие; при точке О - как вертикальные. k=АО:ОС=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. ⇒ Ѕ(АОД):Ѕ(ВОС)=3²=9 ⇒ Ѕ(АОД)=36•9=324.
Высота в ∆ АВО и ВОС общая. Отношение площадей треугольников с равными высотами равно отношению сторон, к которым высоты проведены. Ѕ(АВО)=3Ѕ(ВСО)=36•3)=108 Аналогично Ѕ(СОД)=3Ѕ(ВОС)=108. (попутно заметим, что площади треугольников, образованных частями диагоналей и боковыми сторонами трапеции всегда равны именно по этому свойству). Площадь трапеции АВСД равна сумме площадей четырех треугольников. S(АВСД)=36+324+2•108=576 ( ед. площади)
площадь трапеции равна средняя линия * высоту. Для нахождения высоты опустим перпендикуляр из точки В к стороне АД. Получим точку О. Рассмотрим треугольник АВО, он прямоугольный т.к. ВО перпендикуляр. Угол АВО = 150-90=60 градусов. Находим угол ВАО 90-60=30 градусов. По теореме сторона лежащая против угла 30 градусов равна половине гипотенузы, отсюда ВО=1/2 АВ = 3 см. Находим площадь = 3*10=30см кв